AYT Matematik Karmaşık Sayılar Konu Anlatımı

Gerçek sayıların yetersiz kaldığı durumlarda matematik, yeni bir sayı türü tanımlar:
Karmaşık Sayılar.

Bu sayılar, özellikle 2. dereceden denklemlerin köklerini bulma sürecinde ortaya çıkmıştır.
Bir denklem gerçek kök içermediğinde  çözüm ancak bu yeni sayı sistemiyle mümkündür.

🔎 Tanım:

Karmaşık sayılar,

​

şeklinde yazılır.

Burada:

• a: gerçek kısım

• b: sanal kısım katsayısı
  

📚 AYT’de Sıklıkla Sorgulananlar:

• Karmaşık sayının eşleniği, modu (mutlak değeri)

• Toplama, çıkarma, çarpma, bölme işlemleri

• Karmaşık düzlemde gösterim

• $i$’nin kuvvetleri ve periyodikliği

• 2. dereceden denklemlerin karmaşık kökleri

🔹 Ünitenin Alt Başlıkları:

1. Karmaşık Sayı Tanımı ve i’nin Özellikleri

2. Karmaşık Sayılarda Dört İşlem

3. Karmaşık Sayının Eşleniği ve Mutlak Değeri

4. Karmaşık Sayıların Denkliği

5. Karmaşık Sayıların Görsel Gösterimi (Argüman – Düzlem)

6. Uygulamalı Sorular ve Köklerle İlişkiler

Karmaşık Sayı Tanımı ve i’nin Özellikleri

📘 Karmaşık Sayı Nedir?

Bir karmaşık sayı:

​

şeklinde yazılır.

Burada:

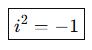
📘 Karmaşık Sayılar Kümesi:

🧠 Gerçek Sayılar ile Farkı:

• denklemine gerçek sayılarda çözüm yok

• Karmaşık sayılarda çözüm:

📘 i’nin Kuvvetleri:

Karmaşık sayıların önemli bir özelliği:
$i$’nin kuvvetleri döngüseldir.

🔁 Genel Kural:

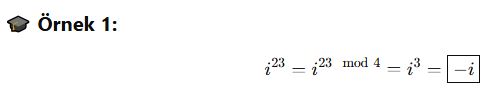
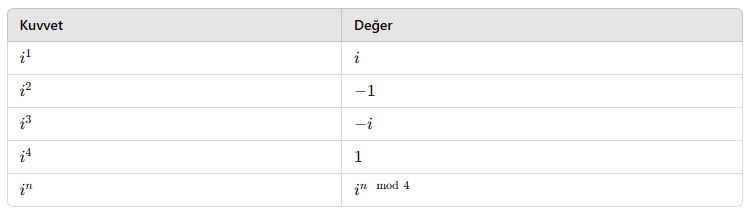
📌 Özet:

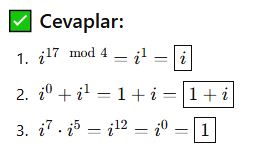
Karmaşık Sayılarda Dört İşlem

📘 A. Toplama ve Çıkarma

Karmaşık sayılar gerçek ve sanal kısımlar kendi arasında işleme girer:

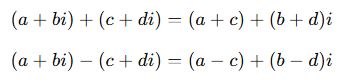
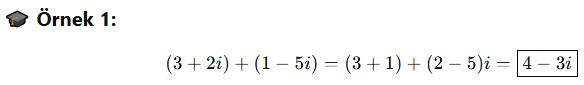
📘 B. Çarpma

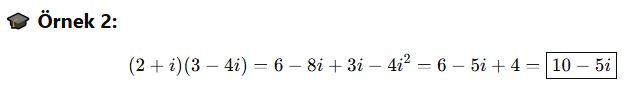
📘 C. Bölme (Eşleniğiyle Çarpma)

Karmaşık sayı bölme işlemi, payda rasyonelleştirilerek yapılır.
Payda karmaşık sayının eşleniğiyle çarpılır.

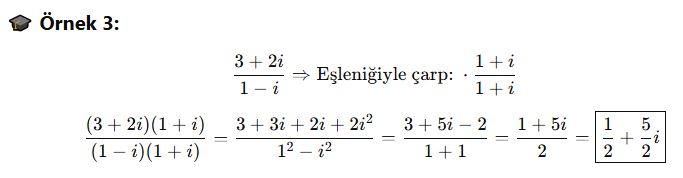
📌 İpuçları:

• Toplama ve çıkarma: benzer terimleri grupla

• Çarpma: 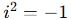 kuralını unutma

• Bölme: eşlenik ile çarp, payda daima gerçek olur

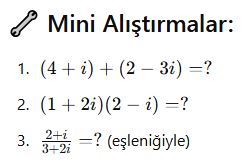
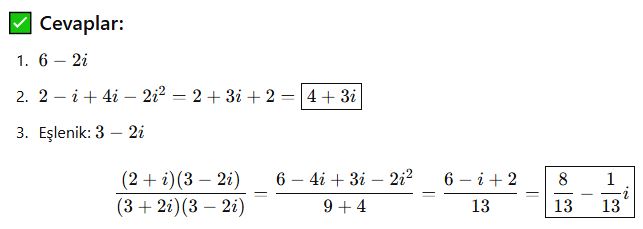
Karmaşık Sayının Eşleniği ve Mutlak Değeri

📘 A. Karmaşık Sayının Eşleniği

Bir karmaşık sayının eşleniği, sanal kısmının işareti değiştirilerek yazılır.

🧠 Eşlenik ile çarpım:

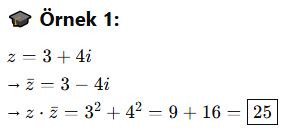
📘 B. Karmaşık Sayının Modülü (Mutlak Değeri)

Karmaşık Sayıların Denkliği

📘 Tanım:

İki karmaşık sayı birbirine eşitse, hem gerçek kısımları hem de sanal kısımları birbirine eşittir.

​

Bu özellik, AYT’de özellikle bilinmeyen içeren denklemlerde kullanılır.

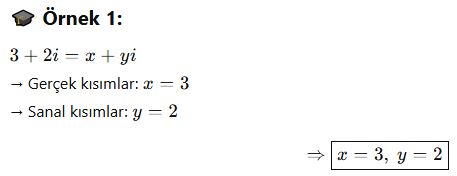
📘 Soru Tipi:

• Bilinmeyenleri içeren karmaşık ifadeler verilir

• Denkliği kullanarak gerçek ve sanal kısımları ayrı ayrı eşitle

• Genellikle iki bilinmeyenli denklem çözümüne döner

📌 Notlar:

• Denkliğin sadece bir kısmı eşit olamaz

• Karmaşık sayılar gerçek sayılar gibi “kümelenmez”

Karmaşık Sayıların Görsel Gösterimi (Argüman – Düzlem)

📘 Karmaşık Düzlem (Gauss Düzlemi)

Karmaşık sayılar, koordinat düzlemine benzer bir yapıda gösterilir:

• Gerçek eksen (x ekseni) → Gerçek kısım (a)

• Sanal eksen (y ekseni) → Sanal kısım (b)

Her z=a+bi karmaşık sayısı, düzlemde bir nokta ya da vektör olarak gösterilir.

📘 Modül (Mutlak Değer) – Tekrar:

📘 Argüman (arg z):

Bir karmaşık sayının argümanı, vektörün pozitif gerçek ekseniyle yaptığı açıdır.
Genellikle radyan cinsinden ifade edilir.

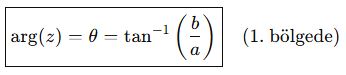
Diğer bölgelerde açıya dikkat edilir!

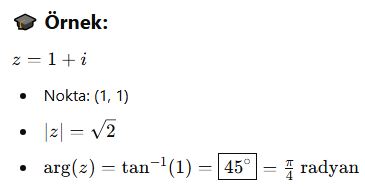
📌 Argüman ile ilgili notlar:

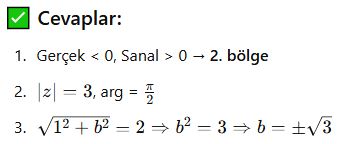
Uygulamalı Sorular ve Köklerle İlişkiler

📘 A. 2. Dereceden Denklemler ve Karmaşık Kökler

Bir 2. dereceden denklemin kökleri:

📘 B. Karmaşık Sayılarla Çarpanlara Ayırma

Bir polinomun karmaşık kökleri varsa çarpanları da buna göre yazılır:

📘 C. Karmaşık Sayıların Üstel Güçleri ve i’li Sorular

Sınavlarda şu tip sorular da gelebilir:

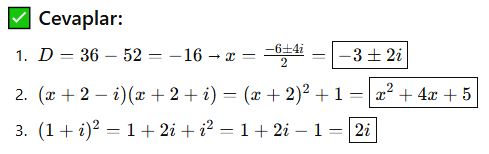
Karmaşık Sayılar Testi

Cevap anahtarı en altta
Her soru farklı bir kazanımı ölçmek üzere hazırlanmıştır.

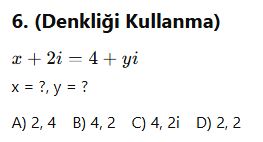
A) 1 B) 2 C) 3 D) 4