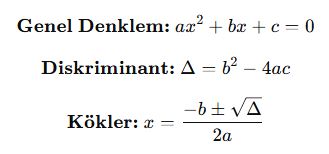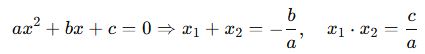AYT Matematik 2.Dereceden Denklemler Konu Anlatımı

2. dereceden denklemler; matematikte kök bulma, fonksiyon grafikleri, paraboller, eşitsizlikler ve karma problemler gibi birçok konunun temelidir.
   AYT’de bu konu özellikle:

• Denklemin tanımı ve yapısı

• Köklerin bulunması

• Köklerin çarpımı ve toplamı

• Diskriminant kavramı

• Gerçek, eşit ve karmaşık kök yorumları

• Kökler üzerine kurulu problemler
  başlıklarıyla çokça karşımıza çıkar.

🔹 Ünitenin Alt Başlıkları:

1. 2.Dereceden Denklemin Tanımı

2. Kök Bulma Yöntemleri

3. Diskriminant ve Köklerin Durumu

4. Kökler ve Katsayılar Arasındaki İlişki

5. Kökler Üzerine Problemler

6. Karmaşık Kökler ve Özel Durumlar

🎯 AYT’de Bu Konu Nasıl Sorulur?

• Verilen denklemin kökleri sorulabilir

• Köklerin toplamı/çarpımı gibi ifadeler istenir

• Diskriminant üzerinden kök durumu yorumlanır

• Köklerle yeni denklem oluşturma gibi problemler gelebilir

• Karmaşık kök içeren sorular çıkar

2. Dereceden Denklemin Tanımı

📘 Tanım:

Genel biçimi şu şekilde olan denklemlere 2. dereceden (kuadratik) denklemler denir:

Burada:

🧠 Terimlerin Anlamı:

📌 Özel Durumlar:

Mini Alıştırmalar:

Aşağıdaki denklemlerde a, b, c değerlerini belirtin ve denklemin 2. dereceden olup olmadığını yazın:

Kök Bulma Yöntemleri

📘 A. Çarpanlara Ayırma Yöntemi

Eğer denklem şu biçimde yazılabiliyorsa:

→ Çarpanlar sıfıra eşitlenerek kökler bulunur:

🎓 Örnek 1:

📘 B. Kök Bulma Formülü (Δ yöntemi)

Her denklem çarpanlarına ayrılamayabilir. Bu durumda kök bulma formülü kullanılır:

🎓 Örnek 2:

​​

📘 C. Tam Kare Açılımı Kullanma

Eğer denklem tam kare açılımına uygunsa:

📌 Özet: Hangi Yöntemi Ne Zaman Kullanmalı?

Diskriminant ve Köklerin Durumu

📘 Diskriminant Nedir?

İkinci dereceden bir denklemde:

Diskriminant (Δ), köklerin sayısını ve türünü belirler:

📌 Δ’nin Yorumu:

🧠 Not: Karmaşık Kökler

Eğer Δ < 0 ise:

Kökler ve Katsayılar Arasındaki İlişki

📘 Genel Denklem:

🎯 Köklerle Katsayılar Arası Formüller:

Bu formüller, kökleri bulmadan doğrudan köklerin toplamını ve çarpımını verir.
Özellikle yeni denklem oluşturma, köklü ifadeli problemler gibi yerlerde çok işe yarar.

Ters Yöntem – Kökler Verilirse Denklem Yazma

Kökleri verilen bir ikinci dereceden denklemi yazmak için:

🎓 Örnek 3:

Kökleri 2 ve 5 olan denklemin kendisi:

Kökler Üzerine Kurulu Problemler

📘 Bu Başlıkta Neler Var?

• Kökler arasında eşitlik / oran / fark verilmesi

• Köklerle denklem oluşturma

• Kökler kullanılarak farklı işlemler tanımlanması

• Verilen toplam / çarpım değerlerinden denklem yazma

🎯 Yöntem: Köklerin Formüllerini Kullanmak

​

→ Köklerin toplamı ve çarpımı üzerinden denklem kurulabilir.

🎓 Örnek 1:

Bir denklemin köklerinin toplamı 5, çarpımı 6 ise denklem nedir?

🎓 Örnek 2:

Bir denklemin köklerinden biri diğerinin 3 katıdır ve köklerin çarpımı 12’dir.
Denklem nedir?

Çözüm:

🎓 Örnek 3:

Bir denklemin kökleri x1 ve x2
Veriliyor:

📘 İleri Düzey Soru Tipi:

Karmaşık Kökler ve Özel Durumlar

📘 Karmaşık Kök Nedir?

Eğer 2. dereceden bir denklemde diskriminant (Δ) negatif çıkarsa:

→ Denklem gerçek kök içermez,
→ Kökler karmaşık sayı olur.

🎯 Genel Kök Formülü (Δ < 0 için):

🧠 Karmaşık Köklerin Özellikleri:

• Gerçek sayı değildirler

• Daima çift halde çıkarlar (eşlenik)

• AYT’de bu kökleri tanımak ve yorumlamak önemlidir (işlem yaptırılmaz)

📌 Özet: Köklerin Durum Tablosu

2.Dereceden Denklemler Testi

Cevap anahtarı en altta.
Her soru bir alt başlıkla ilişkilidir

1. (Tanım – Temel Bilgi)

Aşağıdakilerden hangisi bir 2. dereceden denklem değildir?

2. (Çarpanlara Ayırma)

denkleminin kökleri aşağıdakilerden hangisidir?

A) 2 ve 5
B) –2 ve –5
C) 1 ve 10
D) –1 ve –10

3. (Kök Bulma – Δ yöntemi)

4. (Tam Kare Denklem)

Aşağıdaki denklemlerden hangisinin çakışık (eşit) iki kökü vardır?

5. (Diskriminant Yorumu)

  denklemi için aşağıdakilerden hangisi doğrudur?

A) İki farklı gerçek kök vardır
B) İki çakışık gerçek kök vardır
C) Gerçek kök yoktur
D) Tek bir gerçek kök vardır

6. (Kökler – Katsayı İlişkisi)

  denkleminin köklerinin toplamı ve çarpımı nedir?

A) Toplam: 8, Çarpım: 15
B) Toplam: –8, Çarpım: –15
C) Toplam: 4, Çarpım: 15
D) Toplam: 8, Çarpım: –15

7. (Köklerden Denklem Kurma)

Kökleri 3 ve –2 olan 2. dereceden denklem aşağıdakilerden hangisidir?

8. (Problem – Oran Verilirse)

Köklerinden biri diğerinin 2 katıdır. Kökler toplamı 9 olduğuna göre denklem nedir?

9. (Karmaşık Kökler)

Aşağıdaki denklemlerden hangisinin kökleri karmaşık sayılardır?

10. (Δ Hesaplama)

  denkleminin diskriminantı kaçtır?

A) 0
B) 4
C) 8
D) 12