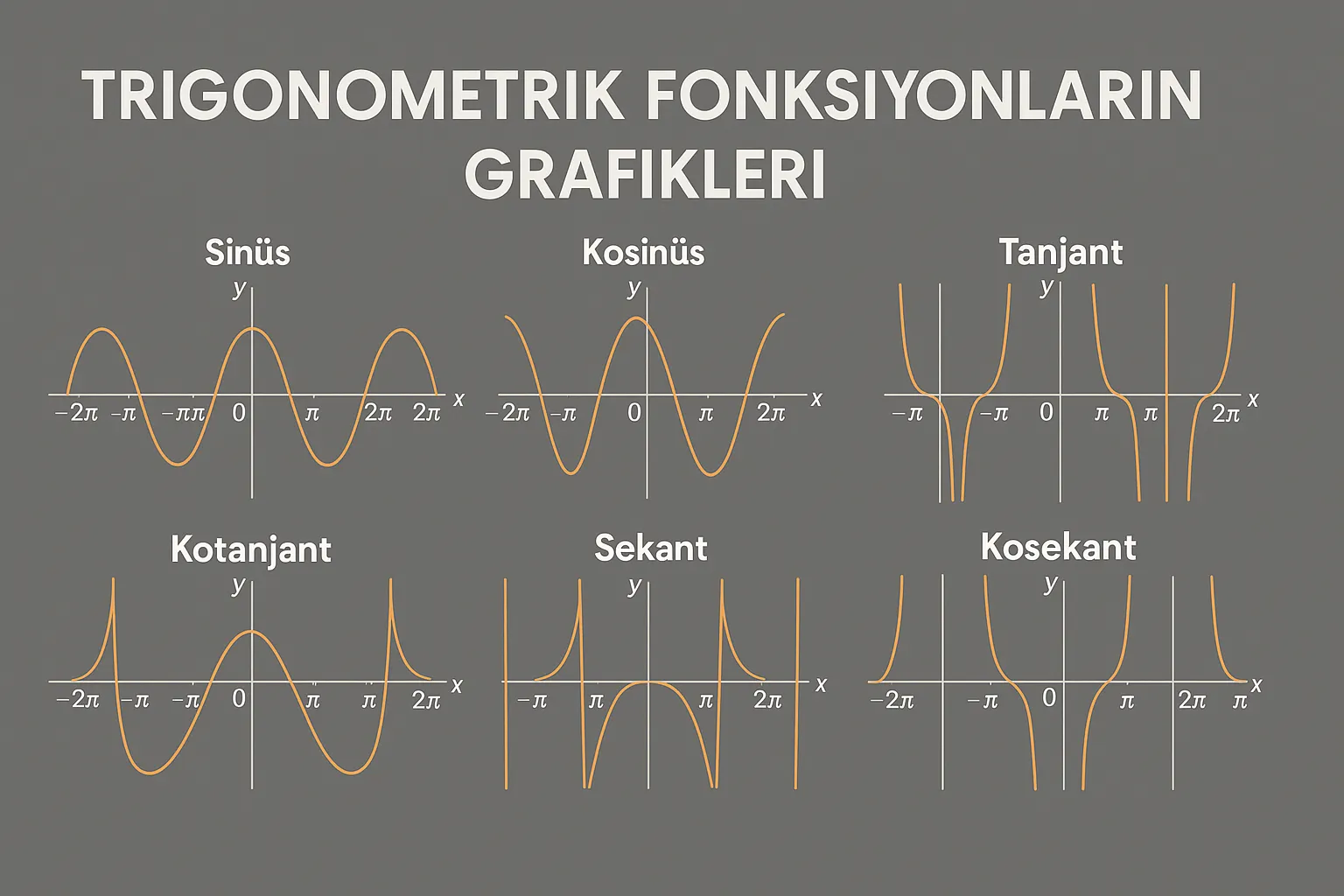
11. Sınıf Matematik Trigonometrik Fonksiyonların Grafikleri Konu Anlatımı ve Örnek Sorular

Trigonometrik Fonksiyonların Grafikleri, 11. sınıf Matematik Trigonometri ünitesinin önemli bir parçasıdır. Bu konuda öğrenciler sinüs, kosinüs, tanjant, kotanjant, sekant ve kosekant fonksiyonlarının grafiklerini detaylıca inceleyerek, birim çember ile grafikler arasındaki ilişkiyi öğrenir. Bu grafiklerin özellikleri, periyotları, genlikleri ve kaymaları öğrencilerin sınav başarısı için kritik konular arasındadır.

Sinüs Fonksiyon Grafiği

Sinüs Fonksiyonunun Özellikleri

Genel form: y = sin(x)
Periyot: 2π
Genlik: 1
Simetri: Orijin etrafında simetrik

Sinüs Fonksiyonunun Grafiği

Sinüs fonksiyonu, y ekseni etrafında dalgalanarak devam eder. En büyük değeri +1, en küçük değeri -1’dir.
Başlangıç noktası (0,0) dır. Grafikte bir tam dalga 2π birim uzunluğundadır.

Kosinüs Fonksiyon Grafiği

Kosinüs Fonksiyonunun Özellikleri

Genel form: y = cos(x)
Periyot: 2π
Genlik: 1
Simetri: Y eksenine göre simetrik

Kosinüs Fonksiyonunun Grafiği

Kosinüs fonksiyonu x = 0 noktasında maksimum +1 değerindedir. Dalga sinüs grafiğine benzer, sadece faz farkı 90° dir. Bir tam dalga 2π birimdir.

Tanjant Fonksiyon Grafiği

Tanjant Fonksiyonunun Özellikleri

Genel form: y = tan(x)
Periyot: π
Dikey asimptotlar: x = ±π/2, ±3π/2, …
Genlik: Yoktur (sınırsız)

Tanjant Fonksiyonunun Grafiği

Tanjant grafiği sürekli artar ve belirli noktalarda tanımsızdır. Dikey asimptotlar bulunur.

Kotanjant Fonksiyon Grafiği

Kotanjant Fonksiyonunun Özellikleri

Genel form: y = cot(x)
Periyot: π
Dikey asimptotlar: x = 0, π, 2π, …
Genlik: Yoktur

Kotanjant Fonksiyonunun Grafiği

Kotanjant grafiği tanjantın tersidir. Grafikte sağdan sola azalır.

Sekant Fonksiyon Grafiği

Sekant Fonksiyonunun Özellikleri

Genel form: y = sec(x) = 1/cos(x)
Periyot: 2π
Dikey asimptotlar: cos(x)=0 olduğu noktalarda

Sekant Fonksiyonunun Grafiği

Kosinüs grafiğinin tanımsız olduğu yerlerde sekant grafiği asimptot oluşturur. Dalgalı parabolik yaylar şeklindedir.

Kosekant Fonksiyon Grafiği

Kosekant Fonksiyonunun Özellikleri

Genel form: y = csc(x) = 1/sin(x)
Periyot: 2π
Dikey asimptotlar: sin(x)=0 olduğu noktalarda

Kosekant Fonksiyonunun Grafiği

Sinüs grafiğinin tanımsız olduğu yerde kosekant grafiği dikey asimptot oluşturur. Parabolik yaylar şeklinde çizilir.

Birim Çember – Grafik İlişkisi

Birim çember, trigonometrik fonksiyonların temelini oluşturur. Açılar birim çemberde ölçülürken fonksiyon grafiklerine yansır. Sinüs y ekseni, kosinüs x ekseniyle ilişkilidir. Tanjant ve diğer fonksiyonlar bu temel oranlardan türetilir.

Mini Deneme Sınavı

1) Sinüs fonksiyonunun periyodu kaçtır?
A) π B) 2π C) 90° D) 180° E) 360°

2) Kosinüs grafiği hangi eksene göre simetriktir?
A) X ekseni B) Y ekseni C) Orijin D) π noktası E) Yok

3) Tanjant fonksiyonunun periyodu nedir?
A) π/2 B) π C) 2π D) 3π E) Yoktur

4) Kotanjant grafiği hangi yöne doğru eğimlidir?
A) Yukarı artar B) Sabit kalır C) Aşağı azalır D) Orijin etrafında döner E) Tanımsızdır

5) Sekant grafiğinde dikey asimptotlar nerede oluşur?
A) sin(x)=0 olduğunda B) tan(x)=0 olduğunda C) cos(x)=0 olduğunda D) cot(x)=0 olduğunda E) Tümünde

Cevap Anahtarı