TYT Matematik Mantık Konu Anlatımı

Mantık, matematiğin temel taşlarından biri olup doğru düşünme ve çıkarım yapma kurallarını içerir. Matematiksel mantık, önermeler, mantıksal bağlaçlar, doğruluk tabloları ve ispat yöntemleri gibi konularla ilgilenir.

Bu ünite, matematiksel ispatların ve akıl yürütme tekniklerinin anlaşılmasını sağlayarak birçok matematiksel problemin çözümünde önemli bir rol oynar. Günlük hayatta ve bilgisayar bilimlerinde de mantık devreleri ve algoritmalar gibi konularda sıkça kullanılır.

1. Önermeler

Önerme, doğru veya yanlış olabilen kesin bir yargı bildiren ifadelerdir.
Örnekler:

• “Ankara Türkiye’nin başkentidir.” (Doğru Önerme ✅)
• “2 çift bir sayıdır.” (Yanlış Önerme ❌)

Önerme olmayan ifadeler:

• “Bugün hava güzel mi?” (Soru cümlesi ❌)
• “Keşke İstanbul’a gitseydim.” (Dilek cümlesi ❌)

Önerme sembol ile gösterilir:

• p: “3 bir asal sayıdır.” (Yanlış)
• q: “7 bir asal sayıdır.” (Doğru)

2. Bileşik Önermeler

Birden fazla önermenin mantıksal bağlaçlarla birleştirilmesiyle oluşan önermelere bileşik önerme denir.

Mantıksal Bağlaçlar

1. Ve Bağlacı (∧) – Kesişim Mantığı
   • p ∧ q bileşik önermesi ancak her iki önerme de doğru olduğunda doğrudur.
   • Örnek:
     • p: “Bugün pazartesi.”
     • q: “Hava güneşli.”
     • p ∧ q: “Bugün pazartesi ve hava güneşli.”
   • Doğruluk Tablosu:

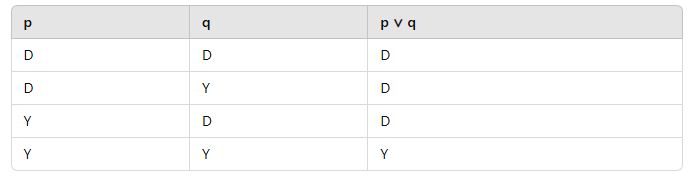
2. Veya Bağlacı (∨) – Birleşim Mantığı

• p ∨ q bileşik önermesi en az bir önerme doğru olduğunda doğrudur.
• Örnek:
  • p: “Bugün pazartesi.”
  • q: “Hava yağmurlu.”
  • p ∨ q: “Bugün pazartesi veya hava yağmurlu.”
• Doğruluk Tablosu:

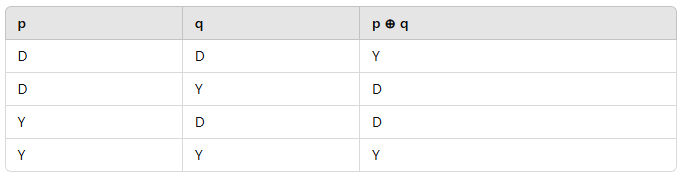
3. Ya Da Bağlacı (⊕) – Ayrıcalıklı Veya

• p ⊕ q, yalnızca biri doğru olduğunda doğrudur.
• Örnek:
  • p: “Ahmet başarılıdır.”
  • q: “Mehmet başarılıdır.”
  • p ⊕ q: “Ya Ahmet başarılıdır ya da Mehmet başarılıdır.”
• Doğruluk Tablosu:

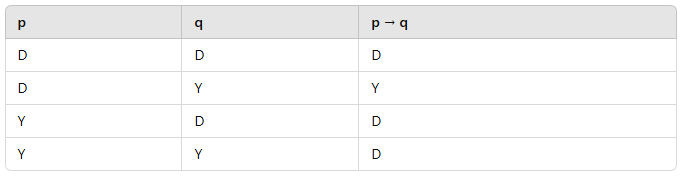
4. İse Bağlacı (→) – Koşullu Önerme

• p → q, p doğru olup q yanlış olduğunda yanlıştır.
• Örnek:
  • p: “Sınava çalışırsam.”
  • q: “Başarılı olurum.”
  • p → q: “Sınava çalışırsam başarılı olurum.”
• Doğruluk Tablosu:

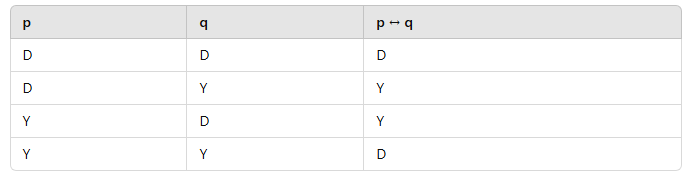
5. Ancak ve Ancak Bağlacı (↔) – Eşdeğerlik

• p ↔ q, her iki önerme aynı doğruluk değerine sahip olduğunda doğrudur.
• Örnek:
  • p: “Ali başarılıdır.”
  • q: “Ali ödül alır.”
  • p ↔ q: “Ali başarılıdır ancak ve ancak ödül alırsa.”
• Doğruluk Tablosu:

3. Totoloji ve Çelişki

4. Açık Önerme ve Niceleyiciler

• Açık Önerme: İçinde bilinmeyen bir değişken bulunan ve bu değişkene bağlı olarak doğru veya yanlış olabilen önermelerdir.
  Örnek: “x bir asal sayıdır.”

• Niceleyiciler:

  • Evrensel Niceleyici (∀): Her x için geçerli olan ifadeler.
    Örnek: “∀x ∈ ℕ, x ≥ 0” (Her doğal sayı sıfırdan büyüktür.)
  • Varlık Niceleyici (∃): En az bir x için doğru olan ifadeler.
    Örnek: “∃x ∈ ℕ, x = 2” (En az bir x değeri 2 olabilir.)

5. Matematiksel İspat ve Yöntemleri

1. Doğrudan İspat:
   
   
2. Tersine İspat (Çelişki Yöntemi):
   
   
3. Tümevarım Yöntemi:
   
   ​

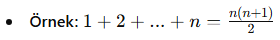
6. Mantığın Elektrik Devrelerinde Kullanımı

Mantıksal bağlaçlar, bilgisayar bilimleri ve elektrik devrelerinde kullanılır.

• “VE” kapısı (AND) → p ∧ q
• “VEYA” kapısı (OR) → p ∨ q
• “DEĞİL” kapısı (NOT) → ¬p

Özet

• Mantık, önermeler ve mantıksal bağlaçları içerir.
• Bileşik önermeler VE, VEYA, İSE gibi bağlaçlarla oluşturulur.
• Matematiksel ispat yöntemleriyle doğruluk gösterilir.
• Mantık devreleri ve bilgisayar bilimlerinde de yaygın olarak kullanılır.

TYT Matematik Mantık Testi

1. Önermeler

Aşağıdaki ifadelerden hangisi bir önerme değildir?
A) 3 asal bir sayıdır.
B) Türkiye’nin başkenti Ankara’dır.
C) 5 bir çift sayıdır.
D) Bugün hava güzel mi?

2. Bileşik Önermeler

Aşağıdaki bileşik önermelerden hangisinin doğruluk değeri her zaman “doğru” olur?
A) p ∧ p’
B) p ∨ p’
C) p → p’
D) p ⊕ p’

3. Ve Bağlacı (∧)

Aşağıda verilen p ve q önermeleri için p ∧ q ifadesi ne zaman doğru olur?
A) p ve q önermelerinden en az biri doğru olduğunda
B) p ve q önermelerinden biri yanlış olduğunda
C) p ve q önermelerinin her ikisi de yanlış olduğunda
D) p ve q önermelerinin her ikisi de doğru olduğunda

4. Veya Bağlacı (∨)

p ve q önermelerinin en az biri doğru olduğunda doğru olan bileşik önerme hangisidir?
A) p ∧ q
B) p → q
C) p ∨ q
D) p ↔ q

5. İse Bağlacı (→)

Aşağıdaki doğruluk tablosu hangi bileşik önermeye aittir?

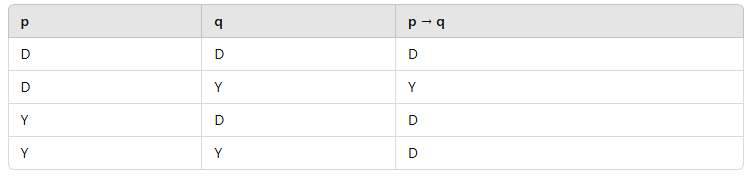
A) p ∧ q
B) p → q
C) p ⊕ q
D) p ↔ q

6. Totoloji ve Çelişki

Aşağıdaki önermelerden hangisi her zaman doğrudur (totolojidir)?
A) p ∧ p’
B) p ∨ p’
C) p ⊕ p’
D) p → p’

7. Niceleyiciler

“Tüm doğal sayılar çift sayıdır.” ifadesinin sembolik gösterimi aşağıdakilerden hangisidir?
A) ∃x ∈ ℕ, x çifttir
B) ∀x ∈ ℕ, x çifttir
C) ∃x ∈ ℕ, x > 0
D) ∀x ∈ ℕ, x tek sayıdır

8. Matematiksel İspat

Matematiksel tümevarım yöntemi hangi tür ifadeleri ispatlamak için kullanılır?
A) Doğru olduğu bilinen ifadeleri
B) Bütün gerçek sayılar için geçerli olan ifadeleri
C) Bütün doğal sayılar için geçerli olan ifadeleri
D) Sadece negatif tam sayılar için geçerli olan ifadeleri

9. Mantığın Elektrik Devrelerinde Kullanımı

Mantıksal devrelerde “VE” kapısının mantıksal karşılığı aşağıdakilerden hangisidir?
A) p ∨ q
B) p ∧ q
C) p ⊕ q
D) p → q

10. Ancak ve Ancak Bağlacı (↔)

Aşağıdaki doğruluk tablosu hangi bileşik önermeye aittir?

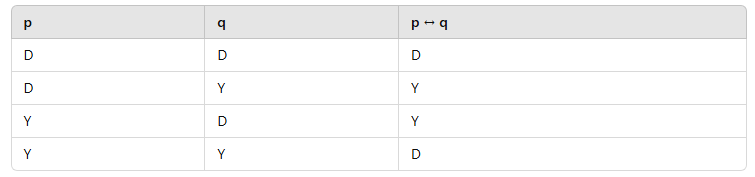
A) p ∨ q
B) p → q
C) p ↔ q
D) p ∧ q

Cevap Anahtarı

1. D
2. B
3. D
4. C
5. B
6. B
7. B
8. C
9. B
10. C