İçindekiler

Kümeler ve Kartezyen Çarpım Konu Anlatımı

Matematikte küme kavramı, belirli nesnelerden oluşan bir topluluk olarak tanımlanır. Kümeler, matematiğin temel yapı taşlarından biri olup mantık, olasılık, fonksiyonlar ve ilişkiler gibi birçok alanda kullanılır.

Bu ünitede, küme tanımı, küme elemanları, kümelerle işlemler, Venn şemaları, alt kümeler ve kartezyen çarpım gibi temel kavramlar ele alınacaktır. Ayrıca, küme problemleri ve günlük hayatta kümelerin kullanımına dair örnekler verilerek konunun pekiştirilmesi sağlanacaktır.

1. Küme Tanımı ve Küme Elemanları

Bir küme, tanımlanabilir nesnelerin bir bütün olarak gösterildiği bir topluluktur. Küme, büyük harflerle (A, B, C gibi) gösterilir ve elemanları süslü parantez içinde belirtilir.

Örnekler:

A = {elma, armut, muz} (Meyve kümesi)
B = {1, 2, 3, 4, 5} (Doğal sayılar kümesi)
C = {x | x, 0 ile 10 arasında bir tam sayıdır} (Ortak özellik yöntemiyle gösterim)

Eleman kavramı:
Bir x elemanının A kümesine ait olduğu “∈” sembolü ile gösterilir.
Örneğin: 3 ∈ B (3, B kümesine aittir), 7 ∉ B (7, B kümesine ait değildir).

2. Boş Küme ve Evrensel Küme

Boş Küme (∅): Hiçbir elemanı olmayan kümedir.
Örnek: D = {x | x, negatif tek doğal sayıdır} → D = ∅
Evrensel Küme (E): Üzerinde işlem yapılan tüm kümeleri içeren büyük kümedir.
Örnek: E = {Doğal Sayılar Kümesi} içinde A = {2, 4, 6} alt kümesi olabilir.

3. Küme Türleri

Eşit ve Denk Kümeler

Eşit Küme: Elemanları birebir aynı olan kümelerdir.
Örnek: A = {1, 2, 3}, B = {3, 1, 2} ise A = B
Denk Küme: Eleman sayıları aynı olan ama içeriği farklı olabilen kümelerdir.
Örnek: X = {a, b, c}, Y = {1, 2, 3} → X ≠ Y, fakat denklerdir.

Sonlu ve Sonsuz Kümeler

Sonlu Küme: Elemanları sayılabilir ve belirli bir sayıda olan kümedir.
Örnek: A = {1, 2, 3, 4, 5}
Sonsuz Küme: Elemanları sayısız ve sınırlandırılamayan kümelerdir.
Örnek: N = {1, 2, 3, 4, …} (Doğal sayılar kümesi)

4. Küme Gösterim Yöntemleri

Liste Yöntemi: Küme elemanları {} içinde sıralanarak yazılır.
Örnek: A = {2, 4, 6, 8}
Ortak Özellik Yöntemi: Kümenin elemanlarını belirleyen bir özellik yazılır.
Örnek: B = {x | x, 2’den küçük doğal sayılar} → B = {0,1}
Venn Şeması: Kümeler, kapalı eğriler (genellikle daireler) içinde gösterilir.

5. Alt Küme ve Alt Küme Sayısı

Bir kümenin alt kümesi, o kümenin bazı veya tüm elemanlarını içeren başka bir kümedir.
A kümesi B kümesinin alt kümesiyse: A ⊆ B
Öz Alt Küme: Kendisi hariç tüm alt kümeleridir.
Alt Küme Sayısı: n elemanlı bir kümenin alt küme sayısı:

6. Kümelerle İşlemler

Kesişim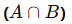

İki kümenin ortak elemanlarını içeren kümedir.
Örnek:
A = {1, 2, 3, 4}, B = {3, 4, 5, 6}

7. Kartezyen Çarpımı

İki kümenin tüm sıralı ikililerinin kümesi olarak tanımlanır.
Tanım:
A ve B kümeleri için:

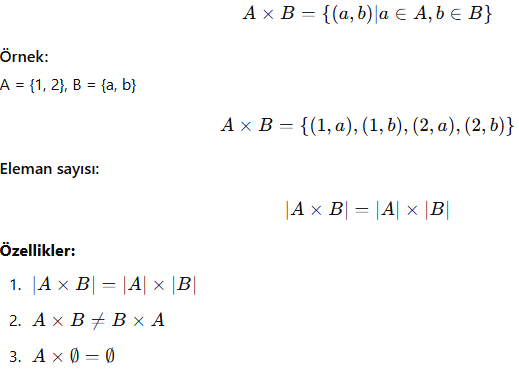
8. Küme Problemleri

Örnek 1: İki Kümenin Kesişimi

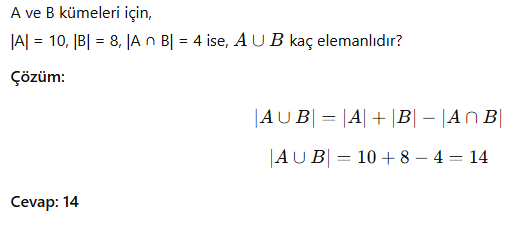
Özet

Kümeler, belirli nesneler topluluğudur.
Alt küme sayısı ile bulunur.
Birleşim, kesişim ve fark işlemleri Venn şeması ile çözülebilir.
Kartezyen çarpımı sıralı ikililerle ifade edilir.

TYT Matematik: Kümeler ve Kartezyen Çarpım Testi

1. Küme Tanımı ve Küme Elemanları

Aşağıdaki ifadelerden hangisi bir küme belirtmez?
A) {Mavi, Kırmızı, Yeşil}
B) {5, 10, 15, 20}
C) {Türkiye’nin en güzel şehri}
D) {x | x bir asal sayıdır}

2. Boş Küme ve Evrensel Küme

A = {x | x, 5 ile 7 arasında tam sayı} kümesi kaç elemanlıdır?
A) 0
B) 1
C) 2
D) 3

3. Alt Küme ve Alt Küme Sayısı

B kümesi {a, b, c} şeklinde tanımlanıyor. B kümesinin toplam kaç alt kümesi vardır?
A) 4
B) 6
C) 8
D) 10

4. Kesişim ve Birleşim İşlemleri

A = {1, 2, 3, 4}, B = {3, 4, 5, 6} kümeleri veriliyor.
A ∩ B kesişim kümesi nedir?
A) {1, 2}
B) {3, 4}
C) {5, 6}
D) {1, 2, 5, 6}

5. Kümelerde Fark İşlemi

A = {1, 2, 3, 4, 5} ve B = {3, 4, 6, 7} kümeleri veriliyor. A – B fark kümesi nedir?
A) {1, 2, 3}
B) {1, 2, 5}
C) {5, 6, 7}
D) {3, 4, 6}

6. De Morgan Kuralları

A ve B iki küme olmak üzere, De Morgan kurallarından biri aşağıdakilerden hangisidir?

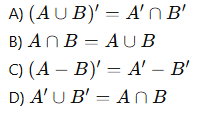
7. Küme Problemleri

Bir sınıfta 40 öğrenci vardır. 25 öğrenci futbol oynuyor, 18 öğrenci basketbol oynuyor ve 10 öğrenci her iki sporu da oynuyor. Futbol veya basketbol oynayan toplam öğrenci sayısı kaçtır?
A) 30
B) 33
C) 35
D) 40

8. Kartezyen Çarpımı

A = {1, 2}, B = {a, b, c} kümeleri veriliyor. A × B kartezyen çarpım kümesinin eleman sayısı kaçtır?
A) 3
B) 4
C) 5
D) 6

9. Kartezyen Çarpımının Özellikleri

A = {0, 1, 2} ve B = {a, b} kümeleri için A × B işlemi kaç elemanlıdır?
A) 2
B) 3
C) 6
D) 8

10. Küme ve Mantık İlişkisi

A kümesi için, A ⊆ B ifadesinin anlamı nedir?
A) A kümesi, B kümesinin elemanıdır.
B) A kümesi, B kümesini kapsar.
C) A kümesi, B kümesinin alt kümesidir.
D) A kümesi, boş kümedir.

Cevap Anahtarı

TYT Matematik Kümeler ve Kartezyen Çarpım Konu Anlatımı ve Örnek Sorular