TYT Matematik Fonksiyonlar Konu Anlatımı

Matematik, birçok farklı kavramın ilişkisini anlamamızı sağlar. Bu ilişkilerin en önemli ve temel yapı taşlarından biri fonksiyonlardır. Fonksiyonlar, bir girdi ile bir çıktı arasındaki belirli bir bağıntıyı tanımlar ve günlük hayatta birçok alanda karşımıza çıkar. Örneğin, bir markette fiyat etiketi, ürünlerin miktarına bağlı olarak toplam maliyeti belirler. Aynı şekilde, bir cismin hızı ile geçen zaman arasındaki ilişki de bir fonksiyon olarak modellenebilir.

Fonksiyonlar, bağımsız değişkenlerin belirli bir kurala göre bağımlı değişkenleri nasıl etkilediğini gösterir. Matematikte fonksiyonları anlamak, denklemler, grafikler ve analiz konularında sağlam bir temel oluşturur. TYT Matematik kapsamında, fonksiyonların tanımı, grafikleri, bileşke ve ters fonksiyonlar gibi birçok önemli kavram detaylı şekilde ele alınacaktır. Bu ünite, sınavda hem doğrudan hem de dolaylı yoldan soru olarak karşımıza çıkabilecek kritik bilgileri içerir.

Fonksiyonları anlamanın en iyi yollarından biri, onları bir makineye benzeterek incelemektir. Bu bakış açısı, fonksiyonların temel mantığını kavramamıza yardımcı olur. Şimdi, fonksiyonları daha iyi anlamak için ilk başlığımıza geçelim.

Fonksiyon – Makine Benzetmesi

Fonksiyonları daha iyi kavrayabilmek için en yaygın metaforlardan biri makine benzetmesidir. Bu benzetmeye göre, bir fonksiyon bir makine gibi çalışır. Fonksiyonun içine bir girdi verildiğinde, makine bu girdiyi işler ve bir çıktı üretir. Örneğin, bir tost makinesini düşünelim. İçine ekmek koyduğumuzda, ısı ve mekanizma sayesinde bize kızarmış ekmek verir. Fonksiyonlar da benzer şekilde, belirli kurallara göre girdileri işler ve çıktı üretir.

Matematiksel olarak fonksiyonlar, genellikle f(x) = işlem şeklinde gösterilir. Burada x bağımsız değişkeni temsil ederken, f(x) bağımlı değişkeni ifade eder. Örneğin, f(x) = 2x + 3 fonksiyonunda x değerine bağlı olarak bir çıktı elde ederiz. Eğer x = 4 alırsak:

Burada x = 4 girdisini fonksiyon makinesine koyduğumuzda, 11 çıktısını elde etmiş oluruz. Bu yüzden fonksiyonları girdi-işlem-çıktı mekanizması olarak düşünebiliriz.

Fonksiyon makinesinin daha iyi anlaşılmasını sağlayacak başka bir örnek olarak sıcaklık dönüşümlerini ele alabiliriz. Örneğin, Fahrenheit’tan Celsius’a dönüşüm fonksiyonu:

Bu fonksiyona F = 50 değerini verdiğimizde:

sonucunu elde ederiz. Yani, 50°F sıcaklık, 10°C’ye eşittir.

Bu benzetmeler, fonksiyonların temel mantığını anlamamız için oldukça faydalıdır. Şimdi, bağımsız ve bağımlı değişkenler kavramına geçerek fonksiyonları daha detaylı inceleyelim.

Bağımsız ve Bağımlı Değişkenler

Fonksiyonların temel mantığını anlamak için bağımsız ve bağımlı değişken kavramlarını iyi kavramak gerekir. Bir fonksiyonun bağımsız değişkeni, fonksiyona verdiğimiz girdiyi temsil ederken, bağımlı değişken ise fonksiyonun sonucunu yani çıktıyı ifade eder. Matematiksel olarak bir fonksiyon f(x) şeklinde gösterildiğinde x bağımsız değişken, f(x) ise bağımlı değişkendir.

Örneğin, f(x) = 3x + 2 fonksiyonunda:

• Bağımsız değişken (x): Fonksiyona verilen değerdir.
• Bağımlı değişken (f(x)): Bağımsız değişkenin fonksiyon kuralına göre işlenmesiyle elde edilen çıktıdır.

Eğer x = 5 olursa,

Burada x = 5 bağımsız değişken, f(5) = 17 ise bağımlı değişkendir.

Günlük hayatta da bağımsız ve bağımlı değişkenler birçok yerde karşımıza çıkar. Örneğin:

• Arabanın hızını belirleyen bir fonksiyon: Hız (bağımsız değişken) arttıkça, gidilen mesafe (bağımlı değişken) artar.
• Maaş hesaplama fonksiyonu: Çalışılan saat (bağımsız değişken) arttıkça, kazanılan maaş (bağımlı değişken) artar.

Fonksiyonların temelinde bu değişkenlerin ilişkisi vardır. Şimdi, fonksiyon olma koşulları başlığı altında, bir bağıntının fonksiyon olup olmadığını nasıl belirleyebileceğimizi inceleyelim.

Fonksiyon Olma Koşulları

Bir bağıntının fonksiyon olup olmadığını belirlemek için bazı temel kurallar vardır. Bir bağıntının fonksiyon olması için her girdi (bağımsız değişken), yalnızca bir çıktıya (bağımlı değişken) karşılık gelmelidir. Yani, bir eleman birden fazla çıktıya sahip olamaz.

Örnek 1:

Bir öğrenciye verilen numaranın ona ait olması bir fonksiyon örneğidir. Örneğin:

• 101 → Ahmet
• 102 → Ayşe
• 103 → Mehmet

Burada her öğrenci numarası (bağımsız değişken), yalnızca bir öğrenci ismiyle (bağımlı değişken) eşleşmiştir. Bu, bir fonksiyondur.

Örnek 2:

Bir kişinin TC kimlik numarası, yalnızca ona özeldir. Her TC kimlik numarası yalnızca bir kişiye aittir. Bu da bir fonksiyon örneğidir.

Ancak, bir kişinin birden fazla telefon numarası olabilir. Eğer her TC kimlik numarasına birden fazla telefon numarası atanıyorsa, bu bir fonksiyon olmaz.

Matematiksel Gösterimle Fonksiyon Olma Durumu

Bir bağıntının fonksiyon olup olmadığını anlamak için eşleme yöntemi veya grafik yöntemi kullanılabilir. Eğer her girdiye yalnızca bir çıktı atanıyorsa, bu bir fonksiyondur. Ancak, bir girdi birden fazla çıktıyla eşleşiyorsa, bu bir fonksiyon değildir.

Örneğin:

• A = {1, 2, 3} ve B = {4, 5, 6} kümeleri verildiğinde f: A → B fonksiyonu aşağıdaki gibi olabilir:
  • f(1) = 4
  • f(2) = 5
  • f(3) = 6

Bu durumda her eleman yalnızca bir çıktıyla eşleştiği için bir fonksiyondur.

Ancak,

• f(1) = 4, 5
• f(2) = 6
• f(3) = 4

şeklinde bir eşleme yapılırsa, f(1) birden fazla çıktıya sahip olduğu için fonksiyon değildir.

Bağıntı ve Fonksiyon Örnekleri

Fonksiyon kavramını daha iyi pekiştirmek için çeşitli bağıntı örneklerini inceleyelim.

Örnek 1: Fonksiyon Olan ve Olmayan Bağıntılar

Aşağıdaki bağıntıları inceleyelim:

1. 
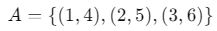
   • Burada her x değeri yalnızca bir y değerine eşlenmiş. Bu bir fonksiyondur.
2. 
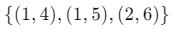
   • Burada 1 değeri iki farklı y değeri ile eşlenmiş. Bu bir fonksiyon değildir.

Örnek 2: Günlük Hayattan Fonksiyon Örnekleri

• Kimlik numarası → Kişi: Her TC kimlik numarası yalnızca bir kişiye ait olduğundan, bu bir fonksiyondur.
• Öğrenci numarası → Okul bölümü: Bir öğrenci numarası sadece bir bölüme kayıtlı olacağından, bu bir fonksiyondur.
• Kişi → Telefon numarası: Bir kişinin birden fazla telefon numarası olabileceğinden, bu bir fonksiyon değildir.

Örnek 3: Grafik Yöntemiyle Fonksiyon Analizi

Bir bağıntının fonksiyon olup olmadığını grafik üzerinde anlamak için dikey doğru testi kullanılır. Eğer bir dikey doğru, grafiği yalnızca bir noktada kesiyorsa, bu bir fonksiyondur. Eğer birden fazla noktada kesiyorsa, bu bir fonksiyon değildir.

Örneğin,

• y = x + 2 fonksiyonunun grafiği çizildiğinde, her x değeri yalnızca bir y değerine karşılık geldiği için bir fonksiyondur.
• x^2 + y^2 = 4 çember denklemi fonksiyon değildir çünkü bazı x değerleri için iki farklı y değeri bulunmaktadır.

Fonksiyon Sayısı

Belirli bir kümeden başka bir kümeye tanımlanabilecek fonksiyonların sayısını bulmak, özellikle kombinatorik problemler açısından önemlidir. Eğer A kümesi m elemanlı ve B kümesi n elemanlıysa, A’dan B’ye tanımlanabilecek tüm fonksiyonların sayısı şu şekilde hesaplanır:

Bu formülün mantığı, A kümesindeki her elemanın B kümesindeki herhangi bir elemana atanabilmesi ilkesine dayanır. Örneklerle açıklayalım:

Örnek 1:

A = {a, b, c} ve B = {1, 2} kümeleri verildiğinde, A’dan B’ye tanımlanabilecek fonksiyon sayısı:

Burada her bir eleman (a, b ve c) bağımsız olarak B kümesindeki 2 farklı elemana atanabilir.

Örnek 2:

Eğer A kümesi 4 elemanlı ve B kümesi 3 elemanlı olsaydı, fonksiyon sayısı:

olurdu.

Fonksiyonların Grafik Gösterimi

Fonksiyonlar, grafiklerle temsil edilerek daha iyi anlaşılabilir. Bir fonksiyonun grafiği, bağımsız değişkenlerin (x) ve bağımlı değişkenlerin (f(x)) bir koordinat sisteminde gösterimiyle elde edilir. Bu grafikler, fonksiyonların davranışını analiz etmek ve çeşitli matematiksel özelliklerini belirlemek için kullanılır.

Örnek: Doğrusal Fonksiyonun Grafiği

Örneğin, f(x) = 2x + 1 fonksiyonunun grafiğini çizmek için çeşitli x değerleri için f(x) değerleri bulunur ve koordinat düzleminde işaretlenir:

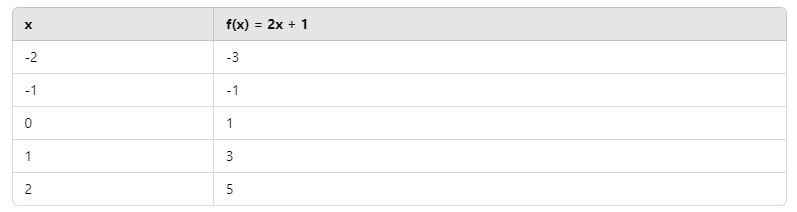
Bu noktalar birleştirildiğinde, doğrusal (linear) bir grafik elde edilir. Doğrusal fonksiyonlar, düz bir doğru şeklinde temsil edilir ve eğimi m ile ifade edilir. Burada m = 2, yani fonksiyon her birim x artışında 2 birim yükselir.

Dikey Doğru Testi

Bir grafiğin fonksiyon olup olmadığını anlamak için Dikey Doğru Testi uygulanır. Eğer her x değeri için yalnızca bir y değeri varsa, grafik bir fonksiyona aittir. Ancak, bir dikey doğru aynı anda iki veya daha fazla noktada kesişiyorsa, bu grafik bir fonksiyon değildir.

Örneğin:

• y = x² fonksiyonunun grafiği bir parabol olup fonksiyondur.
• x² + y² = 4 çember denklemi, bazı x değerleri için iki farklı y değeri içerdiğinden fonksiyon değildir.

Fonksiyon Grafiğini Okuma ve Yorumlama

Bir fonksiyonun grafiğini anlamak, matematiksel ilişkileri görselleştirmeyi sağlar. Grafik üzerinde x ekseni (bağımsız değişken) ve y ekseni (bağımlı değişken) bulunur. Bir fonksiyon grafiğini okurken aşağıdaki temel noktalar dikkate alınmalıdır:

1. Fonksiyonun Tanım Kümesi

Tanım kümesi, fonksiyonun bağımsız değişkeninin alabileceği değerler kümesidir. Grafikte x ekseni boyunca hangi değerlerin kullanıldığını belirleyerek tanım kümesini bulabiliriz.

2. Fonksiyonun Görüntü Kümesi

Görüntü kümesi, fonksiyonun üretebileceği y değerlerinin (çıktılarının) kümesidir. Grafik üzerinde y ekseni boyunca hangi değerlerin alındığını belirleyerek görüntü kümesini bulabiliriz.

3. Kesim Noktaları

• x eksenini kestiği noktalar (kökler): Fonksiyonun f(x) = 0 olduğu noktaları gösterir. Bunlar, fonksiyonun sıfır olduğu yerlerdir.
• y eksenini kestiği nokta: x = 0 olduğunda fonksiyonun aldığı değeri gösterir.

Örneğin, f(x) = x^2 – 4 fonksiyonunun grafiği aşağıdaki gibidir:

• x eksenini x = -2 ve x = 2 noktalarında keser.
• y eksenini y = -4 noktasında keser.

4. Fonksiyonun Artan veya Azalan Olduğu Bölgeler

• Artan Fonksiyon: x arttıkça f(x) de artıyorsa, fonksiyon artan bir fonksiyondur.
• Azalan Fonksiyon: x arttıkça f(x) azalıyorsa, fonksiyon azalan bir fonksiyondur.

Örneğin, f(x) = x^2 fonksiyonu x = 0 noktasında minimum değer alır ve x > 0 bölgesinde artarken, x < 0 bölgesinde azalır.

5. Maksimum ve Minimum Noktalar

Fonksiyonun tepe noktaları (maksimum) ve çukur noktaları (minimum) fonksiyonun en büyük ve en küçük değer aldığı noktaları gösterir. Parabol gibi fonksiyonlarda, bu noktalar önemlidir.

6. Simetri ve Tek-Çift Fonksiyonlar

• Çift Fonksiyonlar: Grafiği y eksenine göre simetrik olan fonksiyonlardır. Örneğin, f(x) = x^2.
• Tek Fonksiyonlar: Grafiği orijine göre simetrik olan fonksiyonlardır. Örneğin, f(x) = x^3.

Örnek Sorular

Soru 1: Aşağıda verilen fonksiyonun tanım ve görüntü kümelerini bulun.

Fonksiyon:

Çözüm:

• Tanım kümesi: x ∈ R (Gerçek sayılar kümesi)
• Görüntü kümesi: y ∈ R (Gerçek sayılar kümesi)

Soru 2: Aşağıdaki fonksiyonun artan veya azalan olduğu bölgeleri belirleyin.

Fonksiyon:

Çözüm: Bu bir ikinci derece fonksiyondur ve parabol şeklindedir. x = -b/2a formülüyle x = 2 noktasında maksimum değere ulaşır.

• x < 2 bölgesinde artan,
• x > 2 bölgesinde azalandır.

Şimdi, Değer Tablosu ile Fonksiyon Grafiği Çizme başlığıyla devam edelim.

Değer Tablosu ile Fonksiyon Grafiği Çizme

Bir fonksiyonun grafiğini oluşturmanın en yaygın yöntemlerinden biri değer tablosu oluşturmaktır. Değer tablosu, belirli x değerlerine karşılık gelen f(x) değerlerini belirleyerek fonksiyonun nasıl davrandığını anlamamıza yardımcı olur.

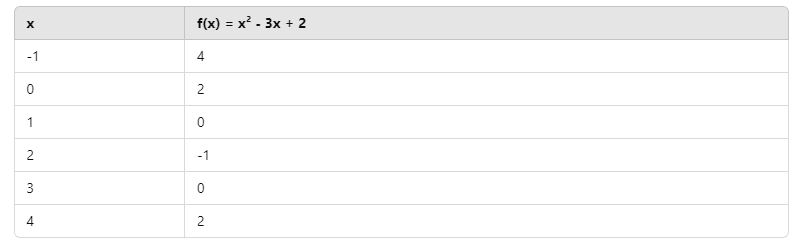
Bu noktalar bir koordinat sistemine yerleştirilerek parabol şeklinde bir grafik elde edilir.

Grafik Çizme Adımları

1. x için bazı değerler seçilir ve f(x) hesaplanır.
2. Elde edilen noktalar koordinat düzleminde işaretlenir.
3. Noktalar birleştirilerek fonksiyonun grafiği oluşturulur.

Değer tablosu kullanarak grafik çizme, fonksiyonun eğimini, artan veya azalan olduğunu ve ekstrem noktalarını belirlemek için önemli bir yöntemdir.

Dikey Doğru Testi

Bir grafiğin bir fonksiyona ait olup olmadığını belirlemek için dikey doğru testi kullanılır. Bu test, her x değeri için yalnızca bir y değeri olup olmadığını anlamamıza yardımcı olur. Eğer bir dikey doğru, grafiği yalnızca bir noktada kesiyorsa, bu grafik bir fonksiyona aittir. Eğer bir dikey doğru, grafiği iki veya daha fazla noktada kesiyorsa, bu grafik bir fonksiyona ait değildir.

Örnekler

1. Fonksiyon Olan Bir Grafik:
   • Doğrusal fonksiyonlar (örn: )
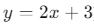   • Parabol fonksiyonları (örn: )
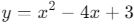   • Mutlak değer fonksiyonu (örn: )
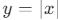   • Üstel fonksiyonlar (örn: )

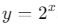   Bu fonksiyonların grafikleri, herhangi bir dikey doğru tarafından yalnızca bir noktada kesilir.

2. Fonksiyon Olmayan Bir Grafik:
   • Çember denklemi (örn: )
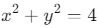   • Dikey çizgiler (örn: )

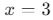   Bu grafikler, bazı x değerleri için birden fazla y değerine sahip olduğundan, fonksiyon değildir.

Uygulama

• Dikey Doğru Testi Nasıl Uygulanır?
  1. Grafiğin herhangi bir yerinden dikey bir çizgi çizin.
  2. Eğer çizgi, grafiği birden fazla noktada keserse, grafik bir fonksiyon değildir.
  3. Eğer çizgi, grafiği yalnızca bir noktada keserse, grafik bir fonksiyondur.

Bu test, fonksiyon olup olmadığını anlamanın en hızlı ve etkili yollarından biridir.

Fonksiyonların Tanım ve Görüntü Kümesi

Bir fonksiyonun tanım kümesi, bağımsız değişkenlerin oluşturduğu kümedir. Yani, fonksiyonun girdi olarak kabul edebileceği tüm değerler tanım kümesini oluşturur. Görüntü kümesi ise fonksiyonun alabileceği çıktılar kümesini ifade eder.

Tanım Kümesi Nasıl Belirlenir?

Tanım kümesini belirlerken aşağıdaki durumlara dikkat edilmelidir:

1. Kesirli ifadeler: Paydanın sıfır olmaması gerekir.
2. Köklü ifadeler: Çift dereceli köklerin içi negatif olmamalıdır.
3. Logaritma fonksiyonları: Logaritma fonksiyonlarında içerik pozitif olmalıdır.

Örnek 1: Fonksiyon:

• Burada paydanın sıfır olmaması gerektiği için x ≠ 3.
• Tanım kümesi:

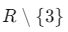
Görüntü Kümesi Nasıl Belirlenir?

Bir fonksiyonun görüntü kümesi, fonksiyonun aldığı tüm y değerlerinden oluşur. Genellikle grafik yöntemi veya cebirsel işlemler ile bulunur.

Örnek 2: Fonksiyon:

• Bu fonksiyon bir parabol olup, en küçük değeri 
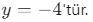
• Görüntü kümesi: 

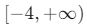
Tanım ve görüntü kümeleri, fonksiyonun hangi değerler için tanımlı olduğunu ve hangi değerleri üretebileceğini belirler.

Tanımsız Noktalar ve Fonksiyonların Sınırlamaları

Bazı fonksiyonlar, belirli x değerleri için tanımsız hale gelebilir. Bu noktalar tanımsız noktalar olarak adlandırılır ve genellikle şu durumlarda ortaya çıkar:

1. Kesirli ifadelerde paydanın sıfır olması: Paydanın sıfır olması matematiksel olarak tanımsızdır.

   Örnek: 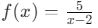  fonksiyonunda x = 2 noktası tanımsızdır.

2. Köklü ifadelerin içinin negatif olması: Çift dereceli köklü ifadelerde içerik negatif olursa reel sayılar kümesinde tanımsız olur.
   • Örnek: 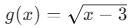fonksiyonunda x ≥ 3 olmalıdır, aksi takdirde tanımsız olur.
3. Logaritma fonksiyonlarında içeriğin negatif veya sıfır olması: Logaritma fonksiyonlarında içerik 0 veya negatif olamaz.
   • Örnek: 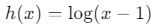fonksiyonunda x > 1 olmalıdır.

Fonksiyonların Sınırlamaları

Fonksiyonlar, belirli aralıklarla sınırlandırılmış olabilir. Bu sınırlamalar genellikle tanım kümesi ve görüntü kümesi ile ilgilidir:

• Tanım Kümesi Sınırlamaları: Fonksiyon yalnızca belirli x değerleri için tanımlıdır.
• Görüntü Kümesi Sınırlamaları: Fonksiyonun alabileceği y değerleri belirli bir aralıkla sınırlandırılmıştır.
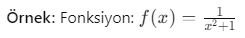
• Tanım kümesi: 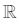(Tüm reel sayılar için tanımlıdır, çünkü payda sıfır olamaz.)
• Görüntü kümesi: 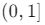(Fonksiyonun minimum değeri 0’a yaklaşırken maksimum değeri 1’dir.)

Fonksiyonların tanımsız noktalarını ve sınırlamalarını belirlemek, fonksiyonun tanım kümesini ve görüntü kümesini doğru anlamak için oldukça önemlidir.

Görüntü Kümesinin Bulunması

Bir fonksiyonun görüntü kümesi, fonksiyonun aldığı tüm çıktı değerlerinden oluşur. Görüntü kümesini belirlemek için çeşitli yöntemler kullanılabilir.

1. Grafik Yöntemi ile Görüntü Kümesi

Eğer bir fonksiyonun grafiği verilmişse, y ekseninde hangi değerlerin alındığını gözlemleyerek görüntü kümesini belirleyebiliriz. Grafiğin en alt ve en üst noktaları görüntü kümesinin sınırlarını belirler.

Örnek: Fonksiyon:

• Bu fonksiyon bir parabol olup en küçük değeri y = -4‘tür.
• Görüntü kümesi:

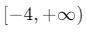
2. Cebirsel Yöntem ile Görüntü Kümesi

Cebirsel yöntem kullanarak, fonksiyonun tersini alıp hangi y değerlerinin mümkün olduğunu belirleyebiliriz. Bunun için fonksiyonun tersi alınır ve tanım kümesi incelenir.

Örnek: Fonksiyon: 

• Bu fonksiyon, x = -2 için tanımsızdır.
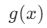• hiçbir zaman sıfır olamaz.
• Ancak tüm diğer pozitif ve negatif değerleri alabilir.
• Görüntü kümesi: 

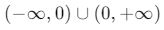
3. Türev Kullanarak Görüntü Kümesi Bulma

Türev kullanarak fonksiyonun artan ve azalan olduğu aralıklar belirlenerek fonksiyonun maksimum ve minimum noktaları bulunur. Bu noktalar görüntü kümesini belirlemede yardımcı olur.

Örnek: Fonksiyon: 

• Türev alarak 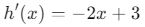 bulunur.
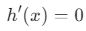• denklemi çözülerek ekstrem nokta bulunur:
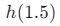• hesaplandığında maksimum y değeri = 7.25 bulunur.
• Parabol aşağıya dönük olduğu için, görüntü kümesi: 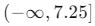olur.

Bu yöntemler kullanılarak, fonksiyonların görüntü kümeleri belirlenebilir. Görüntü kümesi, fonksiyonun hangi çıktı değerlerini alabileceğini anlamak açısından oldukça önemlidir.

Fonksiyon Tipleri

Fonksiyonlar, özel durumlarına göre farklı tiplere ayrılabilir. Bunlar, fonksiyonların matematiksel özelliklerini daha iyi anlamamızı sağlar. Şimdi, başlıca fonksiyon tiplerini inceleyelim.

1. Sabit Fonksiyon

Bir sabit fonksiyon, her x değeri için aynı y değerini üretir. Yani fonksiyon, sabit bir çıktı üretir.

Örnek: Fonksiyon:

• Tüm x değerleri için çıktı 5‘tir.
• Grafiği y ekseni üzerinde yatay bir doğrudur.
• Görüntü kümesi:

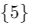
2. Doğrusal Fonksiyon

Doğrusal fonksiyon, bir doğru şeklinde ilerleyen fonksiyondur ve genel formu şu şekildedir:

Örnek: Fonksiyon:

• Eğim 2, y ekseni kesişim noktası 3‘tür.
• Grafiği eğimli bir doğrudur.
• Görüntü kümesi: Tüm reel sayılar,

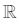
3. Birim Fonksiyon

Birim fonksiyon, her girdiyi kendisine eşleyen fonksiyondur.

Örnek: Fonksiyon:

• Her x, kendisini yansıtacak şekilde çıktı üretir.
• Grafiği orijinden geçen 45° eğimli doğrudur.
• Görüntü kümesi:

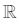
4. Parçalı Fonksiyon

Parçalı fonksiyon, farklı aralıklarda farklı ifadelerle tanımlanan fonksiyondur.

Örnek:

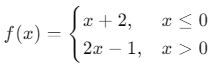
• Grafiği, farklı bölgelerde farklı doğrular içerir.
• Görüntü kümesi, her parça için ayrı hesaplanmalıdır.

5. Örten ve İçine Fonksiyonlar

Bir fonksiyonun örüntü kümesi, tanım kümesinin tüm değerlerini kapsıyorsa örten fonksiyon olarak adlandırılır. Eğer fonksiyonun görüntü kümesi, tanım kümesinden daha küçükse içine fonksiyon denir.

Fonksiyon tipleri, fonksiyonların matematiksel özelliklerini anlamamıza yardımcı olur.

Örten ve İçine Fonksiyonların Grafik Yorumu

Bir fonksiyonun grafik üzerinde örüntü kümesinin tanım kümesini kapsayıp kapsamadığını inceleyerek, fonksiyonun örten veya içine olup olmadığını belirleyebiliriz.

• Örten Fonksiyon: Grafikte, tüm y değerleri için en az bir x değeri bulunuyorsa, fonksiyon örten fonksiyondur.
• İçine Fonksiyon: Eğer fonksiyonun aldığı y değerleri, tüm olası y değerlerinden daha az ise, fonksiyon içine fonksiyondur.

Örnek: Fonksiyon:

• Örten değildir, çünkü sadece pozitif y değerlerini alabilir.
• İçine fonksiyondur, çünkü negatif değerleri kapsamaz.

Bu bölümde, fonksiyonların grafiklerinden örten veya içine olup olmadıklarını nasıl belirleyebileceğimizi inceledik.

Birebir Fonksiyon

Bir fonksiyonun birebir (1-1) fonksiyon olabilmesi için, tanım kümesindeki farklı her x değeri için farklı bir y değeri üretilmelidir. Yani, aynı y değerine sahip iki farklı x değeri olmamalıdır.

Birebir Fonksiyonun Matematiksel İfadesi

Bir f(x) fonksiyonu için aşağıdaki koşul sağlanıyorsa fonksiyon birebirdir:

Bu ifade, eğer f(x_1) = f(x_2) ise x_1 = x_2 olmak zorundadır, yani aynı y değerini farklı x değerleri üretemez.

Birebir Fonksiyon Örnekleri

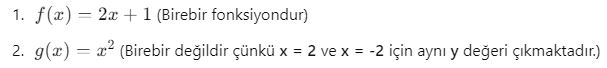
Birebir fonksiyonları anlamak, fonksiyonların tersini bulmada büyük önem taşır. Şimdi, Birebir Fonksiyon Sayısı başlığı ile devam edelim.

Birebir Fonksiyon Sayısı

Bir fonksiyonun birebir fonksiyon sayısını belirlemek, tanım kümesinin eleman sayısı ve fonksiyonun birebir olup olmaması ile ilgilidir. Eğer bir fonksiyon, tanım kümesindeki her farklı x değeri için farklı y değerleri üretiyorsa, bu fonksiyon birebirdir.

Eğer tanım kümesi n elemanlı bir küme ise ve birebir bir fonksiyon tanımlanıyorsa, birebir fonksiyonların sayısı n! (n faktöriyel) kadar olur.

Örnek:

Eğer    kümeleri arasında birebir eşleme yapan fonksiyonlar oluşturulacaksa, bu fonksiyonların sayısı:

olur.

Şimdi, Birebir Fonksiyonların Grafik Yorumu başlığı ile devam edelim.

Birebir Fonksiyonların Grafik Yorumu

Birebir fonksiyonların grafik yorumu, yatay doğru testi ile belirlenebilir. Eğer herhangi bir yatay doğru, fonksiyonun grafiğini en fazla bir noktada kesiyorsa, bu fonksiyon birebirdir.

1. Yatay Doğru Testi

• Bir fonksiyonun birebir olup olmadığını grafik üzerinden kontrol etmek için yatay doğru testi uygulanır.
• Eğer bir yatay doğru, fonksiyonu yalnızca bir noktada kesiyorsa fonksiyon birebirdir.
• Eğer bir yatay doğru fonksiyonu iki veya daha fazla noktada kesiyorsa, fonksiyon birebir değildir.

Örnek: Fonksiyon:

• Kübik fonksiyonun grafiği incelendiğinde, herhangi bir yatay doğru yalnızca bir noktada keser.
• Bu yüzden, 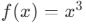    fonksiyonu birebirdir.

Fonksiyon: 

• Parabol fonksiyonu, simetrik bir yapıdadır ve birçok yatay doğru iki farklı noktada grafiği kesebilir.
• Bu nedenle, 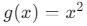    fonksiyonu birebir değildir.

2. Birebir Fonksiyonların Grafikte Temsili

• Artan veya azalan fonksiyonlar genellikle birebirdir.
• Simetrik fonksiyonlar birebir olmayabilir.
• Türev kullanılarak bir fonksiyonun sürekli artan veya azalan olup olmadığı belirlenebilir.

Bu bilgiler ışığında, birebir fonksiyonların grafik yorumlarını anladıktan sonra, şimdi Periyodik Fonksiyonlar başlığı ile devam edelim.

Periyodik Fonksiyonlar

Bir fonksiyon belirli bir periyot aralığında kendini tekrar ediyorsa periyodik fonksiyon olarak adlandırılır. Matematikte, özellikle trigonometri ve dalga hareketlerinde periyodik fonksiyonlar önemli bir yer tutar.

Periyodik Fonksiyonun Tanımı

Bir    fonksiyonunun periyodik olması için, tüm x değerleri için pozitif bir T sayısı bulunmalıdır ki şu koşul sağlansın:

Buradaki , fonksiyonun periyodu olarak adlandırılır.

Periyodik Fonksiyon Örnekleri

1. Sinüs ve Kosinüs Fonksiyonları:
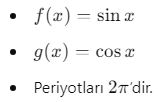
2. Tanjant ve Kotanjant Fonksiyonları:
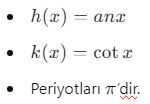
3. Dikdörtgen Dalga Fonksiyonu:
   • Belirli aralıklarla sabit kalan ve aniden değişen fonksiyonlar.

Periyodik fonksiyonlar, fizik ve mühendislikte dalga hareketleri, sinyaller ve titreşimlerde sıkça kullanılır.

Periyodik Fonksiyonlarda Dönüşüm

Periyodik fonksiyonlarda dönüşüm kavramı, fonksiyonun grafiğinin belirli işlemler sonucunda nasıl değiştiğini anlamamıza yardımcı olur. Öteleme, genlik değişimi ve faz kayması gibi dönüşümler, periyodik fonksiyonların farklı görünümlerini incelemek için kullanılır.

1. Dikey ve Yatay Öteleme

Bir periyodik fonksiyon dikey veya yatay olarak ötelenebilir. Öteleme işlemi, fonksiyonun grafik üzerinde yukarı-aşağı veya sağa-sola kaymasını sağlar.

• Dikey Öteleme:
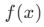  •   fonksiyonuna c sabit bir sayı eklenirse, grafik yukarı veya aşağı kayar.
  • Genel form:
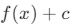
  • Örnek: 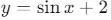  fonksiyonu,  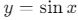  ‘in 2 birim yukarı kaydırılmış halidir.
• Yatay Öteleme:
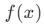  •   fonksiyonunda x yerine (x – c) yazılırsa grafik sağa, (x + c) yazılırsa grafik sola kayar.
  • Genel form:
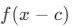
  • Örnek: 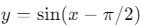  fonksiyonu,  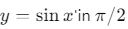  birim sağa kaydırılmış halidir.

2. Genlik Değişimi

Genlik, bir periyodik fonksiyonun maksimum ve minimum değerleri arasındaki mesafeyi belirler. Bir fonksiyonun genliği artırıldığında veya azaltıldığında, dalgaların yüksekliği değişir.

• Genlik artırma veya azaltma:
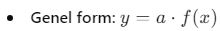
  • Örnek: 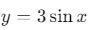   fonksiyonunun genliği 3’tür, yani dalgalar üç kat daha yüksek olur.

3. Periyot ve Frekans Değişimi

Bir periyodik fonksiyonun periyodu, grafiğin belirli bir döngüyü tamamladığı süredir. Periyot, frekans ile ters orantılıdır.

4. Faz Kayması

Faz kayması, periyodik fonksiyonların başlangıç noktasının değişmesi anlamına gelir. Bu, yatay öteleme ile benzer bir etkidir ancak özellikle sinüs ve kosinüs fonksiyonları için önemlidir.

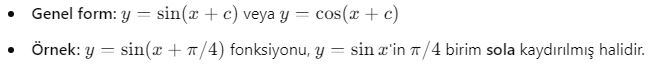
5. Periyodik Fonksiyonlarda Dönüşümün Önemi

• Fizikte dalga hareketlerini anlamak için kullanılır.
• Titreşimler, müzik ve mühendislik uygulamalarında yer alır.
• Dijital sinyal işleme ve görüntü analizinde önemli bir yere sahiptir.

Bu dönüşümler sayesinde periyodik fonksiyonları grafik üzerinde daha kolay yorumlayabilir ve matematiksel modeller oluşturabiliriz.

Periyodik Fonksiyonlar Arasında İşlemler

Periyodik fonksiyonlar arasında işlemler yapılırken, periyot değişimleri ve bileşke fonksiyonlar dikkatlice değerlendirilmelidir. En yaygın işlemler toplama, çıkarma, çarpma ve bileşke fonksiyon işlemleridir.

1. Periyodik Fonksiyonların Toplanması ve Çıkarılması

İki periyodik fonksiyonun toplamı veya farkı genellikle yeni bir periyodik fonksiyon oluşturur. Ancak yeni fonksiyonun periyodu, başlangıçtaki fonksiyonların periyotlarının en küçük ortak katına (EKOK) eşittir.

• Örnek:

2. Periyodik Fonksiyonların Çarpılması

İki periyodik fonksiyonun çarpımı genellikle periyodik bir fonksiyon oluşturur. Periyot, başlangıçtaki periyotların en küçük ortak katı (EKOK) ile bulunur.

• Örnek:

3. Periyodik Fonksiyonların Bileşkesi

İki periyodik fonksiyonun bileşkesi, genellikle orijinal fonksiyonların periyotlarına bağlı olarak değişen bir periyot oluşturur. Bileşke fonksiyonun periyodu ilk fonksiyonun iç fonksiyonun periyoduna nasıl bağlı olduğuna göre belirlenir.

• Örnek:

Bu işlemler, periyodik fonksiyonları daha geniş bir perspektifte değerlendirmemizi sağlar.

Bileşke Fonksiyon

Bileşke fonksiyon, iki veya daha fazla fonksiyonun ardışık olarak uygulanmasıyla elde edilen yeni bir fonksiyondur. Matematiksel olarak, f ve g fonksiyonları verildiğinde, bileşke fonksiyon (f ∘ g)(x) şeklinde gösterilir ve şu şekilde tanımlanır:

Bu ifade, önce g(x) fonksiyonunun hesaplandığını ve ardından elde edilen sonucun f fonksiyonuna uygulandığını gösterir.

1. Bileşke Fonksiyonun Tanım Kümesi

Bileşke fonksiyonun tanımlı olabilmesi için g(x) fonksiyonunun görüntü kümesinin, f(x) fonksiyonunun tanım kümesine dahil olması gerekir. Yani:

Bu koşul sağlanmazsa bileşke fonksiyon tanımsız olur.

2. Bileşke Fonksiyonun Özellikleri

• Bileşke işlemi genellikle değişme özelliğine sahip değildir. Yani, her zaman 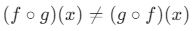    olabilir.
• Bileşke fonksiyonun tanım kümesi, iç fonksiyonun tanım kümesine bağlıdır.
• Bileşke fonksiyonlar zincirleme olarak da tanımlanabilir. Örneğin,    .

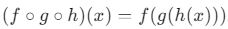3. Bileşke Fonksiyon Örnekleri

Örnek 1:

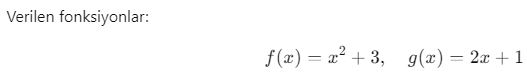
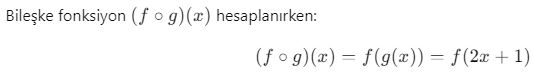
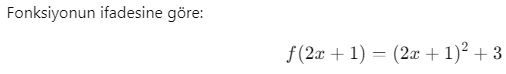
Örnek 2:

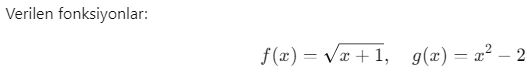
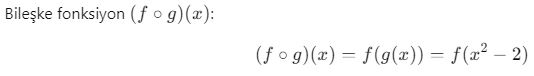
Bu fonksiyonun tanımlı olması için içerideki ifadenin sıfır veya pozitif olması gerekir:

4. Bileşke Fonksiyonun Grafiği

Bileşke fonksiyonun grafiği, adım adım uygulanarak çizilir:

1. İç fonksiyonun (g(x)) grafiği çizilir.
2. Bu değerler dış fonksiyona (f(x)) uygulanır.
3. Ortaya çıkan sonuçlar yeni bir fonksiyon oluşturur.

• Önce g(x) fonksiyonu çizilir.
• Daha sonra her bir g(x) değeri f fonksiyonuna uygulanarak yeni noktalar oluşturulur.
• Yeni fonksiyonun grafiği elde edilir.

Bileşke Fonksiyonun Tanım ve Görüntü Kümesi

Bileşke fonksiyonun tanım kümesi, bileşke işlemi uygulanan fonksiyonların kesişim noktalarına bağlıdır. Öncelikle g(x) fonksiyonunun tanım kümesi belirlenir ve ardından görüntü kümesi, f(x) fonksiyonunun tanım kümesiyle uyumlu olacak şekilde analiz edilir.

Tanım kümesi belirleme adımları:

Görüntü kümesi belirleme adımları:

1. Bileşke fonksiyonun elde edilen sonucu üzerinden f(x) değerleri hesaplanır.
2. Bu değerlerin hangi aralıklarda değiştiği belirlenerek görüntü kümesi oluşturulur.

Örnek:

Fonksiyonlar:

Sonuç olarak, bileşke fonksiyonun tanım kümesi:     olur.

Bileşke Fonksiyonun Grafiği

Bileşke fonksiyonun grafiği, adım adım uygulanarak çizilir. Bu süreçte iç fonksiyonun çıktıları dış fonksiyonun girişleri haline gelir. Aşağıdaki adımlar takip edilerek bileşke fonksiyonun grafiği oluşturulabilir:

1. Adım: İç Fonksiyonun Grafiğini Çizme

İlk olarak, g(x) fonksiyonunun grafiği çizilir. Çünkü bu fonksiyonun çıktıları, bileşke fonksiyonun giriş değerleri olacaktır.

2. Adım: İç Fonksiyonun Değerlerini Dış Fonksiyona Uygulama

İç fonksiyonun çıktıları alınarak, bu değerler dış fonksiyon f(x) üzerinde uygulanır. Yani her x değeri için g(x) hesaplanır ve sonra bu değerler f(x) fonksiyonuna yerleştirilir.

3. Adım: Yeni Noktaları İşaretleme

Elde edilen (x, f(g(x))) noktaları belirlenerek yeni fonksiyonun grafiği oluşturulur.

4. Adım: Grafiğin Doğasını İnceleme

• Grafik sürekli mi?
• Hangi noktalar tanımsız?
• Bileşke fonksiyon artan mı azalan mı?

Örnek: Bileşke Fonksiyon Grafiği Çizme

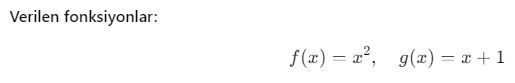
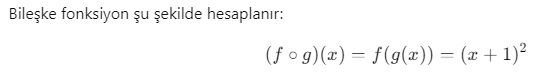
Grafik çizme süreci:

1. g(x) = x + 1 fonksiyonu bir doğru olduğu için her x değeri bir birim sağa kaydırılmıştır.
2. f(x) = x^2 fonksiyonu bir parabol olduğundan, iç fonksiyonun etkisiyle parabol x ekseni üzerinde kayacaktır.
3. Sonuç olarak, yeni fonksiyon (f ∘ g)(x) = (x+1)^2 olarak bir birim sola kaydırılmış bir parabol oluşturacaktır.

Bu yöntem, bileşke fonksiyonların grafiklerini anlamak ve çizmek için kullanılan temel süreçtir.

Üç Fonksiyonun Bileşkesi

1. Üç Fonksiyonun Bileşkesinin Tanım Kümesi

Üç fonksiyonun bileşkesi tanımlanırken, fonksiyonların birbirine uygulanabilir olması gerekir. Bu nedenle aşağıdaki şartlar sağlanmalıdır:

• h(x) fonksiyonunun tanım kümesi belirlenmelidir.
• h(x)‘in görüntü kümesi g(x) fonksiyonunun tanım kümesine dahil olmalıdır.
• g(h(x)) fonksiyonunun görüntü kümesi f(x) fonksiyonunun tanım kümesine dahil olmalıdır.

Bu koşullar sağlanmazsa bileşke fonksiyon tanımsız olur.

2. Üç Fonksiyonun Bileşkesinin Özellikleri

• Bileşke işlemi genellikle değişme özelliğine sahip değildir. Yani, 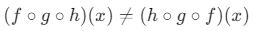   olabilir.
• Üç fonksiyonun bileşkesi adım adım hesaplanmalıdır.
• Tanım kümesi belirlenirken iç içe fonksiyonların geçişleri dikkate alınmalıdır.

3. Üç Fonksiyonun Bileşkesine Örnekler

Örnek 1:

Verilen fonksiyonlar:

Üç fonksiyonun bileşkesi (f ∘ g ∘ h)(x) hesaplanırken:

Önce h(x) hesaplanır:

Sonuç, g(x) fonksiyonuna uygulanır:

Son olarak, f(x) fonksiyonuna uygulanır:

Bu durumda, (f ∘ g ∘ h)(x) = 4x^2 + 4x + 2 olarak bulunur.

Örnek 2:

Verilen fonksiyonlar:

Bileşke fonksiyon şu şekilde hesaplanır:

Önce h(x) hesaplanır:

Sonuç, g(x) fonksiyonuna uygulanır:

Son olarak, f(x) fonksiyonuna uygulanır:

Burada, fonksiyonun tanımlı olabilmesi için kök içindeki ifadenin negatif olmaması gerekir. Bu nedenle:

Bu eşitsizliğin çözümlenmesi sonucunda, uygun tanım kümesi belirlenir.

4. Üç Fonksiyonun Bileşkesinin Grafiği

Üç fonksiyonun bileşkesi grafik çizimi için aşağıdaki adımlar takip edilir:

1. En içteki fonksiyonun (h(x)) grafiği çizilir.
2. h(x) fonksiyonunun çıktıları g(x) fonksiyonuna uygulanır ve yeni noktalar belirlenir.
3. Son olarak g(h(x)) değerleri f(x) fonksiyonuna uygulanarak grafik tamamlanır.

Örnek: Üç Fonksiyonun Bileşkesi Grafiği

Verilen fonksiyonlar:

Bileşke fonksiyon şu şekilde hesaplanır:

Bu yeni fonksiyonun grafiği, (2x + 1)^2 fonksiyonunun grafiğiyle aynıdır. Ancak iç fonksiyonların etkisiyle x ekseni boyunca kayma ve genişleme meydana gelir.

Bu yöntemle, üç fonksiyonun bileşkesi grafiksel olarak analiz edilebilir.

Parçalı Fonksiyonların Bileşkesi

Parçalı fonksiyonların bileşkesi, farklı aralıklarda farklı kurallarla tanımlanan fonksiyonların bileşkelerinin nasıl hesaplanacağını anlamak için önemlidir. Bir parçalı fonksiyonun bileşkesi hesaplanırken, her bir parça ayrı ayrı değerlendirilmelidir.

1. Parçalı Fonksiyonun Tanımı

Bir parçalı fonksiyon, farklı aralıklarda farklı matematiksel ifadelerle tanımlanan fonksiyondur:

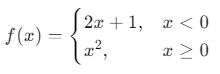
Bir bileşke fonksiyon hesaplanırken, her bir parçanın hangi aralıkta tanımlı olduğu dikkate alınmalıdır.

2. Parçalı Fonksiyonun Bileşkesi Nasıl Hesaplanır?

Bileşke fonksiyon hesaplanırken, iç fonksiyonun her bir parçası ayrı ayrı dış fonksiyona uygulanır.

Örnek:

Verilen fonksiyonlar:

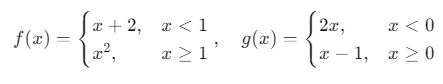
Sonuç olarak, bileşke fonksiyon şu şekilde tanımlanır:

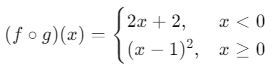
Bu hesaplamalar, parçalı fonksiyonların bileşkesiyle ilgili problemlerde dikkat edilmesi gereken adımları gösterir.

Bileşke Fonksiyon İşlem Özellikleri

Bileşke fonksiyonlar belirli matematiksel kurallara ve özelliklere sahiptir. Bu özellikler, fonksiyonlarla yapılan işlemlerde önemli bir yer tutar.

1. Değişme Özelliği

Genel olarak bileşke fonksiyonlar değişme özelliğine sahip değildir. Yani, aşağıdaki ifade genellikle doğru değildir:

Örnek:

Fonksiyonlar:

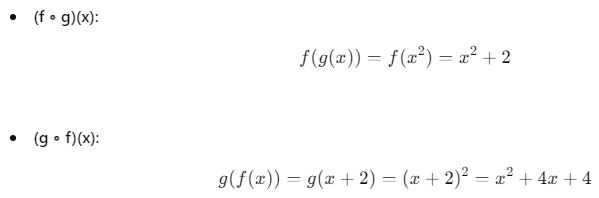
Görüldüğü gibi, (f ∘ g)(x) ≠ (g ∘ f)(x)’tir.

2. Birim Fonksiyon Özelliği

Eğer bir f(x) fonksiyonunun g(x) fonksiyonu ile bileşkesi birim fonksiyon oluşturuyorsa, bu durumda şu ilişki sağlanır:

Birim fonksiyon, herhangi bir girdiyi doğrudan çıktıya dönüştüren f(x) = x fonksiyonudur.

3. Ters Fonksiyon Özelliği

Eğer f(x) ve g(x) fonksiyonları birbirinin ters fonksiyonlarıysa, bileşkeleri birim fonksiyon olur:

Bu özellik, fonksiyonların tersini bulmada kullanılır.

Bileşke Fonksiyonların Örten ve Birebir Olma Durumları

Bir fonksiyonun birebir (injektif) olması, farklı girdilerin farklı çıktılar üretmesi anlamına gelir. Öte yandan, bir fonksiyon örten (surjektif) olması için, hedef kümedeki her elemanın en az bir karşılığı olmalıdır.

1. Birebir (İnjektif) Bileşke Fonksiyonlar

Eğer g(x) ve f(x) fonksiyonları birebir ise, bileşke fonksiyon (f ∘ g)(x) de birebirdir. Ancak, yalnızca f(x) birebir olup g(x) birebir değilse, bileşke fonksiyon birebir olmayabilir.

Örnek:

Fonksiyonlar:

• f(x) doğrusal bir fonksiyondur ve birebirdir.
• g(x) = x^3 fonksiyonu artan bir fonksiyon olduğu için birebirdir.
• (f ∘ g)(x) = 2(x^3) + 3 = 2x^3 + 3 fonksiyonu da birebirdir.

Ancak, g(x) = x^2 gibi birebir olmayan bir fonksiyon kullanılsaydı, bileşke fonksiyon da birebir olmayacaktı.

2. Örten (Surjektif) Bileşke Fonksiyonlar

Bir bileşke fonksiyonun örten olması için, dış fonksiyonun örten olması yeterli değildir; iç fonksiyonun da uygun bir görüntü kümesine sahip olması gerekir.

Örnek:

Fonksiyonlar:

• g(x) doğrusal bir fonksiyon olduğu için örten olabilir.
• Ancak, f(x) = x^2 fonksiyonu yalnızca pozitif değerler üretebildiği için, bileşke fonksiyon (f ∘ g)(x) = (2x+1)^2 negatif değerleri kapsamaz.
• Sonuç olarak, bileşke fonksiyon örten değildir.

Eğer f(x) fonksiyonu da tüm reel sayıları kapsayabilseydi, bileşke fonksiyon örten olabilirdi.

3. Hem Birebir Hem Örten (Bijektif) Bileşke Fonksiyonlar

Bir bileşke fonksiyon hem birebir hem de örten ise, bijektif fonksiyon olur. Bijektif fonksiyonların tersi her zaman tanımlıdır.

Örnek:

Fonksiyonlar:

• Her iki fonksiyon da birebir ve örtendir.
• Bileşke fonksiyon (f ∘ g)(x) = 3(x+2) – 5 = 3x + 6 – 5 = 3x + 1 de bijektif olur.

Bu bölümde bileşke fonksiyonların birebir ve örten olma durumlarını inceledik.

Ters Fonksiyon

Bir fonksiyonun tersi, verilen fonksiyonun çıktısını tekrar girdiye dönüştüren fonksiyondur. Bir fonksiyonun tersi f⁻¹(x) ile gösterilir ve şu özelliği sağlar:

Ters fonksiyonun var olabilmesi için fonksiyonun birebir ve örten (bijektif) olması gerekir. Eğer bir fonksiyon bijektif değilse, ters fonksiyonu tanımsız olur.

1. Ters Fonksiyonun Tanımlanması

Bir fonksiyonun tersini bulmak için aşağıdaki adımları takip edebiliriz:

1. Fonksiyonun y = f(x) şeklinde yazılması
2. x ve y’nin yer değiştirilmesi
3. Yeni denklemin x cinsinden çözülmesi
4. Ters fonksiyonun f⁻¹(x) olarak ifade edilmesi

2. Ters Fonksiyonun Grafik Üzerindeki Yorumu

Bir fonksiyonun ters fonksiyonunun grafiği, y = x doğrusuna göre simetriktir. Yani, f(x) fonksiyonundaki herhangi bir (a, b) noktası, f⁻¹(x) fonksiyonunda (b, a) noktası olarak bulunur.

Örnek:

Fonksiyonun grafiği aşağıdaki gibi olsun:

• f(x) = 2x + 3 fonksiyonu çizilir.
• Ters fonksiyon f⁻¹(x) = (x – 3)/2 fonksiyonunun grafiği çizilir.
• Bu iki grafik y = x doğrusuna göre simetrik olur.

3. Ters Fonksiyonun Tanım ve Görüntü Kümesi

Bir fonksiyonun tersinin tanım kümesi, orijinal fonksiyonun görüntü kümesidir. Benzer şekilde, ters fonksiyonun görüntü kümesi de orijinal fonksiyonun tanım kümesidir.

Örnek:

Burada, f(x) = x^2 fonksiyonunun x ≥ 0 koşulu ile verilmesi önemlidir. Çünkü tüm reel sayılar için bu fonksiyon birebir olmazdı ve ters fonksiyon tanımsız olurdu.

4. Bileşke Fonksiyon ile Ters Fonksiyonun İlişkisi

Bir fonksiyonun kendisiyle bileşkesinin ters fonksiyonu vermesi şu şekilde gösterilir:

Bu ilişki, fonksiyonların ters fonksiyon olup olmadığını test etmek için kullanılabilir.

5. Ters Fonksiyonun Uygulama Alanları

• Kriptografi: Şifreleme algoritmalarında kullanılır.
• Fizik ve Mühendislik: Bir sistemin giriş-çıkış ilişkisini anlamak için.
• Ekonomi ve Finans: Talep ve arz eğrileri gibi analizlerde.

Bu bölümde ters fonksiyonun tanımını, nasıl bulunacağını ve grafik üzerindeki ilişkisini inceledik.

Ters Fonksiyonun Grafiği

Ters fonksiyonun grafiği, orijinal fonksiyonun y = x doğrusuna göre simetrisi olarak çizilir. Bunun anlamı, ters fonksiyonun her noktası orijinal fonksiyonun noktalarının koordinatları değiştirilerek elde edilir.

Örnek:

Bu yöntemi kullanarak herhangi bir fonksiyonun tersinin grafiğini çizebiliriz.

Temel Fonksiyonların Tersi

Matematikte bazı fonksiyonlar, özellikle sık kullanılan temel fonksiyonlar için ters fonksiyonların doğrudan belirlenmesi önemlidir. Temel fonksiyonların tersi, genellikle standart kurallar ve işlemler yardımıyla hesaplanabilir.

1. Lineer Fonksiyonların Tersi

Lineer fonksiyonlar, f(x) = ax + b şeklinde ifade edilir. Ters fonksiyonunu bulmak için şu adımları izleyebiliriz:

Örnek:

Fonksiyon verilsin:

Bu, tüm reel sayılar için tanımlıdır.

2. Üstel ve Logaritmik Fonksiyonların Tersi

Örnek:

3. Kare ve Karekök Fonksiyonlarının Tersi

• Kare fonksiyonunun tersi karekök fonksiyonudur. Ancak mutlak değer alınarak tanım kümesi dikkate alınmalıdır:
  
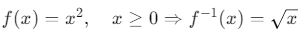
• Karekök fonksiyonunun tersi kare fonksiyonudur:
  

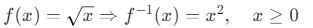
Örnek:

4. Trigonometrik Fonksiyonların Tersi

Ters trigonometrik fonksiyonlar belirli aralıklarla sınırlıdır, çünkü trigonometrik fonksiyonlar periyodiktir ve birebirliği sağlamak için uygun aralık seçilmelidir.

Bu bölümde temel fonksiyonların terslerini ve nasıl bulunacaklarını inceledik.

Parçalı Fonksiyonların Tersi

Parçalı fonksiyonlar, farklı aralıklarda farklı kurallarla tanımlanan fonksiyonlardır. Ters fonksiyonlarını bulmak için her parçayı ayrı ayrı değerlendirmek gerekir. Bir parçalı fonksiyonun tersi bulunurken, her parçanın birebir olması ve ters fonksiyonunun da belirli bir aralıkta tanımlanması gerekir.

1. Parçalı Fonksiyonun Tersini Bulma

Parçalı fonksiyonun tersini bulmak için aşağıdaki adımlar izlenir:

1. Her parçanın birebir olup olmadığını kontrol et.
2. Parçaları ayrı ayrı tersine çevir.
3. Her parçanın tanım ve görüntü kümelerini değiştir.
4. Parçalı fonksiyonun tersi olarak yeni bir parçalı fonksiyon yaz.

2. Parçalı Fonksiyonun Tersine Örnek

Verilen parçalı fonksiyonun tersini bulalım:

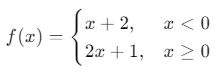
Her parçanın tersini bulalım:

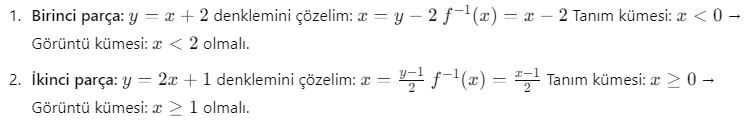
Sonuç:

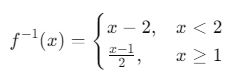
Bu parçalı fonksiyonun tersi olarak tanımlanır.

3. Parçalı Fonksiyonların Tersinin Grafiği

Bir parçalı fonksiyonun tersi, y = x doğrusuna göre simetrik olacak şekilde çizilir. Her parçanın tanım kümesi, görüntü kümesiyle değiştirildiğinde, fonksiyonun yeni grafiği elde edilir.

Örnek: Fonksiyon verilsin:

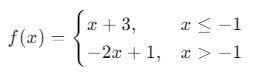
Bu fonksiyonun tersini bulduktan sonra grafiği şu şekilde çizilir:

1. Her parçanın tersini al.
2. Yeni tanım kümelerini düzenle.
3. Orijinal fonksiyonun grafiğini y = x doğrusuna göre simetrik olarak çevir.

Sonuç olarak, parçalı fonksiyonların tersi belirlenirken dikkat edilmesi gereken en önemli nokta, her parçanın birebir olması ve ters fonksiyonun da bir parçalı fonksiyon olarak tanımlanması gerektiğidir.

Bu bölümde parçalı fonksiyonların tersini bulmayı öğrendik.

Fonksiyonlarla İşlemler

Fonksiyonlarla yapılan işlemler, temel aritmetik işlemlerden türev ve integral gibi ileri düzey işlemlere kadar geniş bir yelpazeye sahiptir. TYT Matematik’te genellikle toplama, çıkarma, çarpma ve bölme işlemleri üzerinde durulmaktadır.

1. Fonksiyonların Toplanması ve Çıkarılması

İki fonksiyon f(x) ve g(x) verildiğinde, bu fonksiyonların toplamı ve farkı şu şekilde tanımlanır:

Örnek:

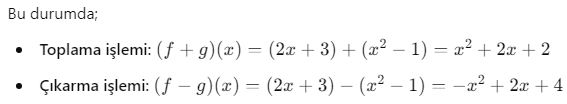
2. Fonksiyonların Çarpımı

İki fonksiyon çarpılırken, her bir fonksiyonun değerleri birbirleriyle çarpılır:

Örnek:

Bu durumda;

3. Fonksiyonların Bölümü

İki fonksiyonun bölümü, pay ve paydanın ilgili fonksiyon değerleri üzerinden hesaplanmasıyla tanımlanır:

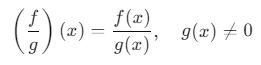
Burada g(x) ≠ 0 olmalıdır, aksi takdirde fonksiyon tanımsız olur.

Örnek:

Fonksiyonların bölümü şu şekilde hesaplanır:

Paydaki ifadeyi çarpanlarına ayıralım:

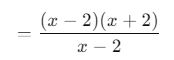
Payda ve paydayı sadeleştirdiğimizde:

Sonuç olarak, g(x) ≠ 0 olduğu için noktasında fonksiyon tanımsızdır.

Bu kural, rasyonel fonksiyonlarda kritik noktaların belirlenmesine yardımcı olur.

4. Fonksiyonların Birleşik İşlemleri

Bileşke işlemleriyle birlikte fonksiyonlar toplama, çarpma ve bölme gibi işlemlere tabi tutulabilir. Ancak işlemler yapılırken tanım kümeleri dikkatlice incelenmelidir.

Örnek:

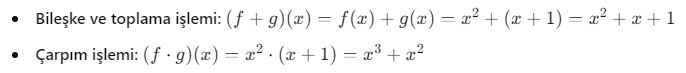
Özel Fonksiyonel İlişkiler

Matematikte bazı fonksiyon türleri, özel ilişkiler ve özellikler taşır. Bu özel fonksiyonlar belirli durumlarda önemli kolaylıklar sağlar.

1. Sabit Fonksiyon

Bir fonksiyonun tüm girdileri için aynı çıktıyı verdiği durumda sabit fonksiyon oluşur. Matematiksel olarak şu şekilde tanımlanır:

Sabit fonksiyonun grafiği, x eksenine paralel düz bir doğrudur.

Örnek:

Bu fonksiyonun tüm x değerleri için çıktısı 5‘tir.

2. Doğrusal Fonksiyon

Doğrusal fonksiyon, değişkenin sabit bir katsayı ile çarpılıp bir sabit eklenmesiyle elde edilen fonksiyondur:

Burada a eğimi, b ise y eksenini kestiği noktayı ifade eder.

Örnek:

Bu fonksiyon bir doğrusal fonksiyondur ve grafiği eğimli bir doğru olacaktır.

3. Birim Fonksiyon

Birim fonksiyon, değişkenin kendisini çıktıya veren fonksiyondur:

Bu fonksiyonun grafiği y = x doğrusudur.

4. Mutlak Değer Fonksiyonu

Mutlak değer fonksiyonu, girdinin negatif olması durumunda pozitif yapan özel bir fonksiyondur:

Bu fonksiyonun grafiği, V şeklindedir.

Örnek:

Bu fonksiyonun grafiği x = 3 noktasında simetriktir.

5. İşaret Fonksiyonu

İşaret fonksiyonu, bir girdinin pozitif, negatif veya sıfır olup olmadığını belirleyen bir fonksiyondur:

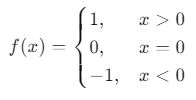
Bu fonksiyon, özellikle limit ve türev konularında önemli bir yere sahiptir.

6. Periyodik Fonksiyon

Belirli bir T periyodunda tekrar eden fonksiyonlara periyodik fonksiyon denir. Matematiksel olarak:

7. Tek ve Çift Fonksiyonlar

• Tek fonksiyonlar, f(-x) = -f(x) eşitliğini sağlayan fonksiyonlardır. Grafikleri orijin etrafında simetriktir.
• Çift fonksiyonlar, f(-x) = f(x) eşitliğini sağlayan fonksiyonlardır. Grafikleri y ekseni etrafında simetriktir.

Örnek:

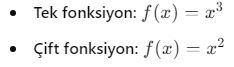
Fonksiyonların Uygulama Alanları

Fonksiyonlar, matematiksel modeller oluşturmak ve gerçek dünyadaki olayları analiz etmek için birçok alanda kullanılır. İşte fonksiyonların başlıca kullanım alanları:

1. Fizik ve Mühendislik

Fonksiyonlar, fiziksel olayları modellemek ve mühendislik hesaplamalarında kullanılır. Hareket denklemleri, elektrik devreleri ve mekanik sistemlerde önemli bir rol oynar.

• Hareket Denklemleri: 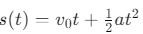    Burada s(t) konum fonksiyonu, v₀ başlangıç hızı, a ivme ve t zaman değişkenidir.
• Elektrik Devreleri: 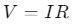   Ohm yasasına göre voltaj, akım ve direnç arasındaki ilişki fonksiyonlarla modellenir.

2. Ekonomi ve Finans

Fonksiyonlar, fiyat değişimleri, arz-talep dengesi ve yatırım modellerini analiz etmek için ekonomide yaygın olarak kullanılır.

• Arz ve Talep Fonksiyonları: 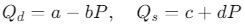 ,  Burada Qd talep edilen miktar, Qs arz edilen miktar, P fiyat ve a, b, c, d katsayılardır.
• Faiz Hesaplamaları: 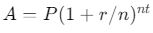   Burada A toplam miktar, P ana para, r faiz oranı, n yıllık bileşik faiz sayısı ve t yıl sayısıdır.

3. Biyoloji ve Tıp

Fonksiyonlar, biyolojik büyüme modelleri, popülasyon dinamikleri ve ilaç etkilerini analiz etmek için kullanılır.

• Popülasyon Modelleri: 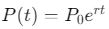   Burada P(t) popülasyon büyüklüğü, P₀ başlangıç popülasyonu, r büyüme oranı ve t zamandır.
• İlaç Dağılımı: 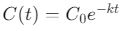   Kan dolaşımındaki ilaç miktarı, vücutta zamanla azalan bir fonksiyon olarak ifade edilir.

4. Bilgisayar Bilimleri ve Yapay Zeka

Fonksiyonlar, algoritmaların ve veri analizlerinin temel yapı taşlarını oluşturur.

• Mantıksal Fonksiyonlar:
  
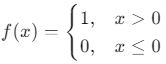
  Yapay sinir ağlarında aktivasyon fonksiyonu olarak kullanılır.
• Şifreleme ve Kriptografi: 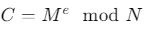 Burada C şifreli metin, M açık metin, e şifreleme üssü ve N modüler değerdir.

5. Grafik Tasarımı ve Animasyon

Fonksiyonlar, bilgisayar grafiklerinde ve animasyonlarda nesnelerin hareketlerini modellemek için kullanılır.

• Bezier Eğrileri: 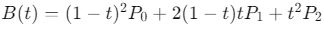 Grafik tasarımda eğri modelleme için kullanılır.
• Fizik Motorları: Nesnelerin hareketlerini ve çarpışmalarını simüle etmek için fiziksel denklemler kullanılır.

6. Coğrafya ve Meteoroloji

Fonksiyonlar, hava tahmini, iklim değişiklikleri ve topoğrafik analizlerde kullanılır.

• Sıcaklık Değişimleri: 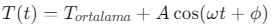 Burada T(t) sıcaklık değişimi, A genlik, ω açısal frekans ve φ faz kaymasıdır.
• Rüzgar Hızı ve Basınç İlişkisi: Meteoroloji analizlerinde diferansiyel fonksiyonlar kullanılarak tahminler yapılır.

Bu bölümde,

Fonksiyonlarla İlgili Çıkmış Soru Örnekleri

Fonksiyonlarla ilgili çıkmış sorular, konunun sınavlarda nasıl ele alındığını görmek açısından oldukça önemlidir. Aşağıda, geçmiş yıllarda çıkmış ve benzeri örnekler üzerinden detaylı çözümlerle desteklenmiş sorular yer almaktadır.

Fonksiyonlarla İlgili Test

Aşağıda, fonksiyonlarla ilgili bilgilerinizi pekiştirebileceğiniz kapsamlı bir test yer almaktadır. Her soru farklı bir konuyu kapsayarak, TYT sınavında çıkabilecek soru tiplerini yansıtmaktadır.