İçindekiler

AYT Matematik Parabol Konu Anlatımı

Parabol, AYT Matematik müfredatında önemli bir yer tutar ve özellikle fonksiyonlar, denklemler ve geometri ile ilişkilidir. Bu konu anlatımı, parabolün tanımını, özelliklerini ve denklemlerini ele alır. Parabolün genel formu, tepe noktası, simetri ekseni, ve kesişim noktaları gibi temel kavramları detaylı bir şekilde açıklar. Ayrıca, parabolün grafik üzerinde nasıl çizildiği ve çeşitli problemlerde nasıl kullanıldığı örnek sorularla desteklenmiştir. Bu kaynak, parabolün anlaşılmasını kolaylaştırarak, sınavda karşılaşabileceğiniz soru tiplerine yönelik kapsamlı bir hazırlık yapmanıza yardımcı olacaktır.

Ayrıca bu konu anlatımını bitirdikten sonra sizler için hazırladığımız Parabol testlerini de çözebilirsiniz:

Parabol, 2. dereceden bir fonksiyonun grafiğidir.
Yani:

Bu grafik, simetrik ve U şeklinde bir eğridir.
→ a > 0 ise yukarı bakan
→ a < 0 ise aşağı bakan bir şekil elde edilir.

AYT’de bu konuda:

Tepe noktası
Simetri doğrusu
Kolların yönü
x ve y eksenleriyle kesişim
Grafikten denklem yazma veya yorum yapma
gibi çok yönlü kazanımlar öne çıkar.

🔹 Ünitenin Alt Başlıkları:

Parabolün Tanımı ve Temel Özellikleri
Parabolün Kolları, Tepe Noktası ve Simetri Doğrusu
Parabolün x ve y Eksenleriyle Kesişimi
Parabolün Grafiği ve Yorumu
Tepe Noktası Bilinen veya Geçen Noktaları Verilen Parabol
Parabolün Analitik Düzlemde Uygulamalı Soruları

Parabolün Tanımı ve Temel Özellikleri

📘 Parabol Nedir?

Bir 2. dereceden fonksiyonun grafiği parabol olarak adlandırılır.
Genel denklemi:

Bu grafik:

Simetriktir
Tek tepe noktası veya çukur noktası vardır
Eksensel simetri gösterir
Kolları yukarı veya aşağı bakar

📘 Parabolün Temel Özellikleri:

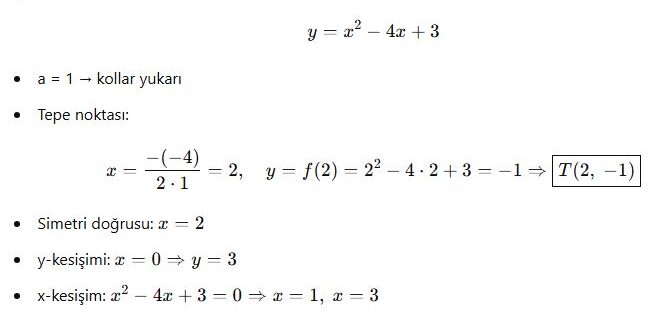
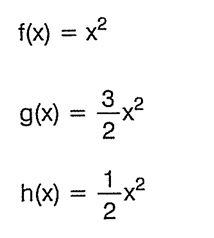
fonksiyonlarının grafiklerini çizelim.

Çözüm:
Fonksiyonların görüntüsünü, x in değişen değerlerine göre bulalım.

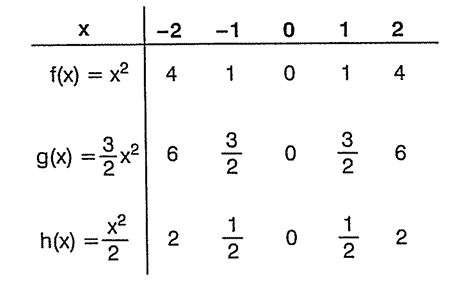
Bulunan noktaları düzlemde işaretleyerek, fonksiyonların grafiklerini çizelim:

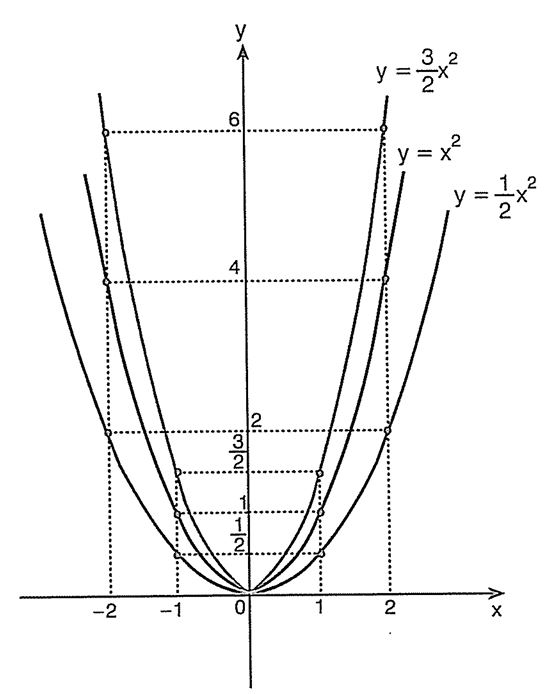
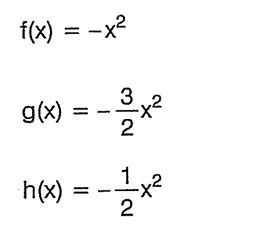
fonksiyonlarının grafiklerini çizelim.

Çözüm:
Fonksiyonların görüntüsünü, x in değişen değerlerine göre bulalım.

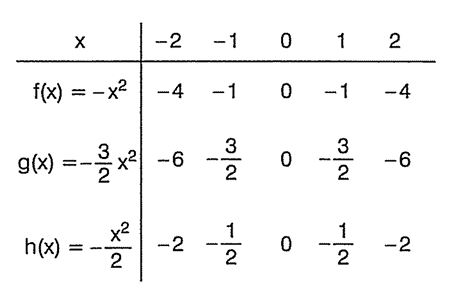
Bulunan noktaları düzlemde işaretleyerek fonksiyonların grafiklerini çizelim:

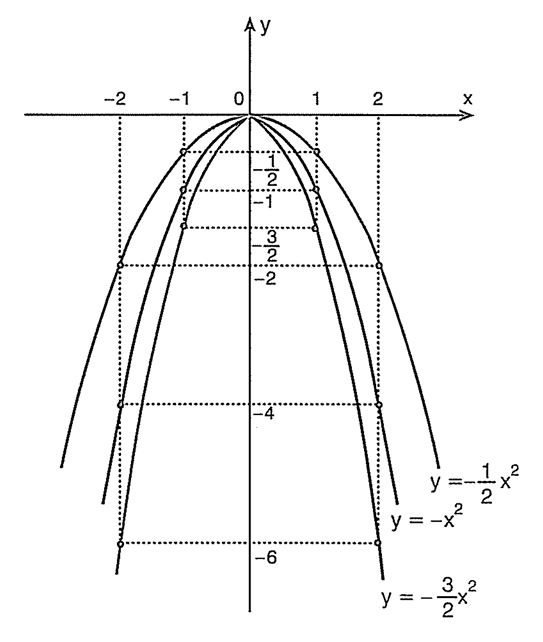
y = ax² parabolü tepe noktası orijinde olan bir paraboldür.
y = ax² parabolünde a > 0 ise kollar yukarı doğrudur.
y = ax² parabolünde a < 0 ise kollar aşağı doğrudur.
y = ax² parabolünde |a| büyüdükçe kolların açıklığı azalır, yani kollar birbirine yaklaşır.

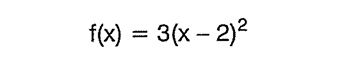
parabolünün grafiğini çizelim.

Çözüm:
f(x) = 3x² parabolünü çizdikten sonra, parabolü x ekseni üzerinde x-2 = 0 => x = 2 birim öteleyerek çizelim.

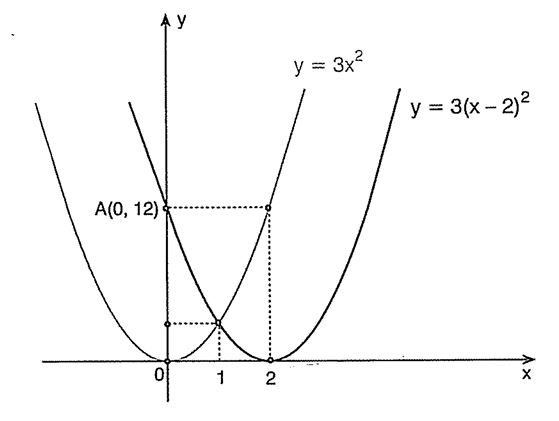
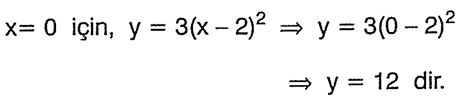
Buna göre, parabol y eksenini A(0, 12) noktasında keser.

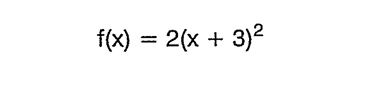
parabolünün grafiğini çizelim.

Çözüm:
f(x) = 2x² parabolünü çizdikten sonra, parabolü x ekseni üzerinde, x + 3 = 0 => x = -3 birim öteleyerek çizelim.

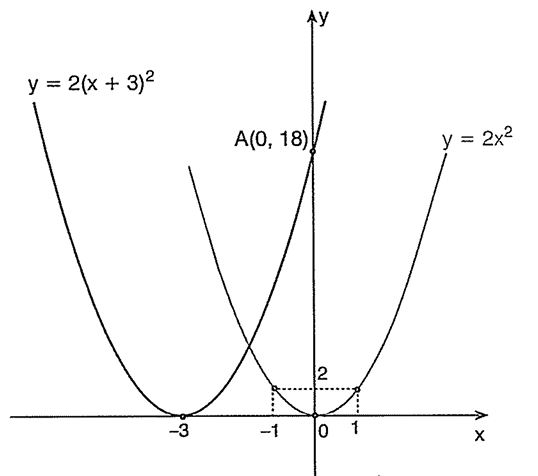
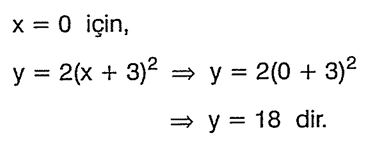
Buna göre, parabol y eksenini A(0, 18) noktasında keser.

📌 Notlar:

Parabolün şekli yalnızca a katsayısına bağlıdır
Simetri doğrusunun solundaki ve sağındaki noktalar aynı y değerini verir
Parabolün tepe noktası, aynı zamanda en küçük veya en büyük değer veren noktadır

Parabolün Kolları, Tepe Noktası ve Simetri Doğrusu

📘 A. Parabolün Kolları

a > 0 → Kollar yukarı bakar
a < 0 → Kollar aşağı bakar
Bu, fonksiyonun minimum veya maksimum değeri olup olmadığını da belirler:
- Yukarı bakan parabol → en küçük değeri vardır
- Aşağı bakan parabol → en büyük değeri vardır

📘 B. Tepe Noktası (T)

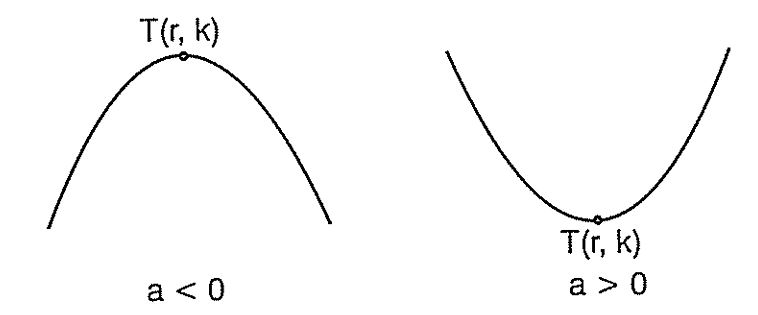
Parabolün a < 0 için en büyük değerini veren T(r, k) noktasına veya a > 0 için en küçük değerini veren T(r, k) noktasına parabolün tepe noktası denir.

f(x) = a(x – r)² + k parabolünün tepe noktasının koordinatları T(r, k) dır.
f(x) = ax² + bx + c parabolünün tepe noktası T(r, k) olmak üzere,

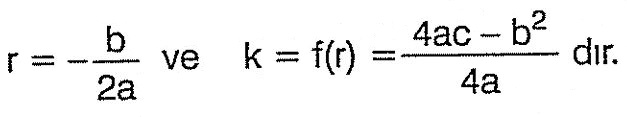
Parabolün en uç noktasıdır.
x ekseni üzerinde:

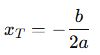
Fonksiyonda yerine yazarsak,

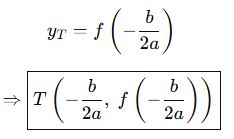
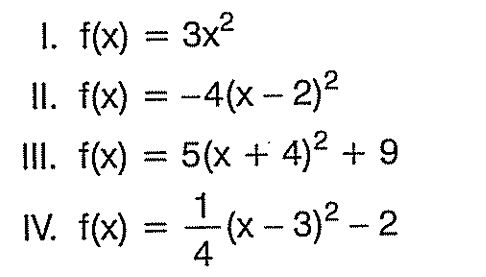
Yukarıdaki parabollerin tepe noktalarını bulalım.

📘 C. Simetri Doğrusu

Parabolün tepe noktasından geçen ve parabolü tam ortadan ikiye bölen düşey doğru.

Aynı x değerine sahip simetrik noktaların y değerleri eşittir.

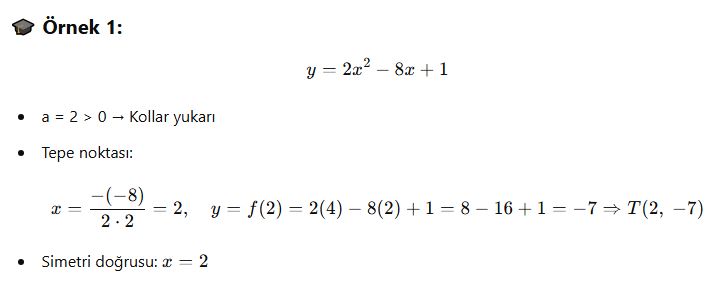
🎯 Özellik Özeti:

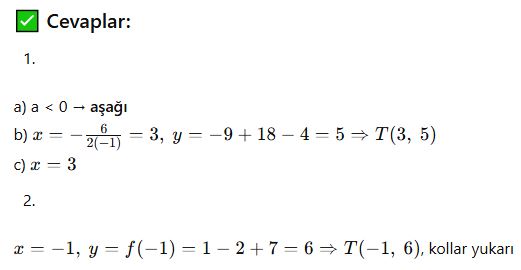
Parabolün x ve y Eksenleriyle Kesişimi

📘 A. y Eksenini Kestiği Nokta

y ekseni üzerindeki tüm noktalarda $x = 0$ ‘dır.

Bu nedenle parabolün y ekseniyle kesiştiği nokta:

çünkü

📘 B. x Eksenini Kestiği Nokta(lar)

x ekseni üzerindeki tüm noktalarda $y = 0$ ‘dır.

Yani parabolün x ekseniyle kesiştiği noktaları bulmak için:

Gerçek ve farklı iki kök → parabol x eksenini iki farklı noktada keser
Gerçek ve çakışık kök → tepe noktası eksene teğettir
Gerçek kök yoksa → parabol x eksenini kesmez

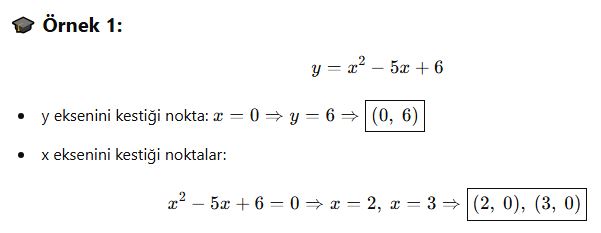
📘 Kesişim Bilgisiyle Parabol Çizimi

Eksenleri kestiği noktalar ve tepe noktası, parabolü çizmek için yeterli referans sağlar.

Parabolün Grafiği ve Yorumu

📘 Grafik Okuma ve Yorumlama Becerisi

AYT’de parabol grafiği verilerek ya da istenerek şu yorumlar yapılabilir:

Tepe noktasından a’nın işareti
x ve y ekseni kesim noktalarından katsayı ilişkileri
Simetri doğrusunun konumu
Grafikteki en küçük/en büyük değer
Grafik üzerinden denklemi oluşturma

📘 Grafiğe Göre Fonksiyon Denklemi Bulma

Kökler biliniyorsa:

Tepe noktası ve bir nokta biliniyorsa:

Verilen başka bir nokta kullanılarak a bulunur

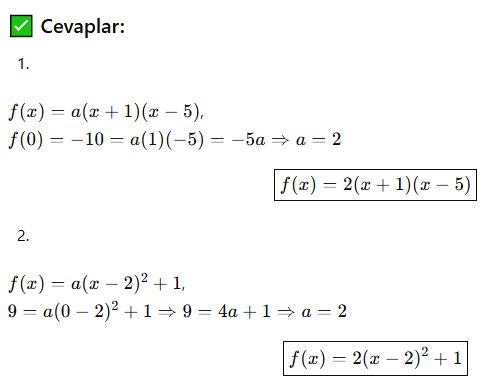
Tepe Noktası Bilinen veya Geçen Noktaları Verilen Parabol

📘 A. Tepe Noktası Biliniyorsa

Eğer parabolün tepe noktası biliniyorsa,
fonksiyon şu şekilde yazılır:

Bu form, parabolün simetrisini ve yönünü doğrudan gösterir.
Eğer parabolün geçtiği başka bir nokta da verilirse, a sabiti belirlenebilir.

📘 B. Parabolün Geçtiği Noktalar Veriliyorsa

Üç farklı nokta veriliyorsa:

Genel denklem: 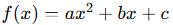yazılır
Her bir nokta için yerine yazılıp, 3 bilinmeyenli denklem sistemi çözülür
→ Bu yöntem grafik çizimi sorularında da çok kullanılır

📘 Kökler ve Tepe Noktasını Kullanma (Gelişmiş Yöntem)

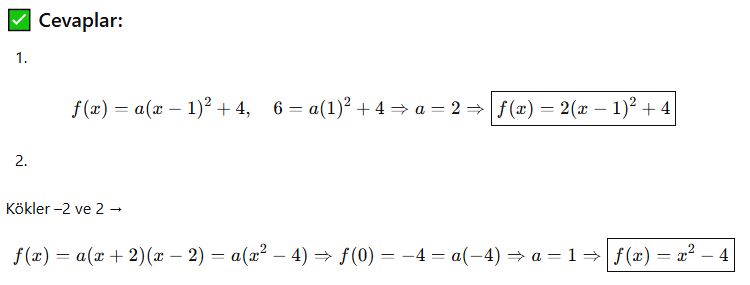
Parabolün Analitik Düzlemde Uygulamalı Soruları

📘 A. Grafik Üzerinden Yorum Soruları

Grafikte parabol verilerek;

Kolların yönü
Tepe noktası
Eksenlerle kesişim
Simetri noktaları
f(x) en küçük/en büyük değer
Belirli bir aralıkta artan/azalan olduğu aralıklar
f(a) < f(b) gibi karşılaştırmalar
sorulabilir.

📘 B. En Küçük / En Büyük Değer Soruları

Tepe noktası verilen ya da bulunabilen parabolde:

olarak bulunur.

📘 C. Aralıkta Artan/Azalan Olma

Tepe noktasına kadar: Azalan
Tepe noktasından sonra: Artan

📘 D. İki Fonksiyonun Kesiştiği Nokta Sayısı

denklemine dönüştürülür
→ denklem çözülür
→ kök sayısı, kesim noktası sayısını verir

Parabol AYT Deneme Testi

(Cevap anahtarı en altta)

1.

parabolünün kolları hangi yöne bakar?

A) Aşağı
B) Yukarı
C) x eksenine paralel
D) Dikey doğru olur

2.

parabolünün tepe noktası nedir?

A) (3, 1)
B) (2, 2)
C) (3, –1)
D) (–3, 1)

3.

parabolü x eksenini keser mi?

A) İki noktada keser
B) Tek noktada keser
C) Kesmez
D) x eksenine teğettir

4.

A) 0
B) 2
C) 4
D) b’ye bağlıdır

7.

Parabol x eksenini hangi noktalarda keser?

A) (2, 0) ve (4, 0)
B) (–2, 0) ve (–4, 0)
C) (1, 0) ve (3, 0)
D) (0, 2) ve (0, 4)

8.

parabolünün en büyük değeri nedir?

A) 4
B) 5
C) 3
D) 6

AYT Matematik Parabol Konu Anlatımı ve Örnek Sorular