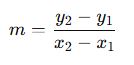10. Sınıf Matematik Analitik İnceleme Konu Anlatımı ve Örnek Sorular

Analitik geometri, cebir ile geometrinin birleştiği bir alandır. Bu ünitede; düzlemde iki nokta arasındaki uzaklık, orta nokta, doğru denklemleri ve doğrular arasındaki konum ilişkileri gibi konular ele alınacaktır. Analitik yöntemler sayesinde geometrik şekiller; koordinat düzlemine taşınır, sayılarla ifade edilir ve cebirsel yollarla incelenebilir.

Analitik İnceleme Konu Anlatımı

10. Sınıf Matematik Analitik İnceleme ünitesi, özellikle doğrunun analitik incelenmesi, eğim, doğruların birbirine göre durumları, paralellik, diklik, ve noktanın doğruya uzaklığı gibi konuları kapsamaktadır.

1. İki Nokta Arasındaki Uzaklık ve Orta Nokta Formülü

📌 A) İki Nokta Arasındaki Uzaklık

Koordinat düzleminde A(x1,y1) ve B(x2,y2) noktaları arasındaki uzaklık şu formülle hesaplanır:

​

Bu formül aslında Pisagor teoreminin analitik düzlemdeki uygulamasıdır.

✅ Örnek:
A(1,2) ve B(4,6) noktaları arasındaki uzaklık:

B) Orta Nokta Formülü

İki noktanın orta noktası, bu noktaların x ve y koordinatlarının aritmetik ortalamasıdır:

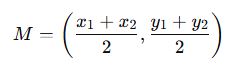
✅ Örnek:
A(2,3) ve B(6,7) noktalarının orta noktası:

Örnek Soru:

A(0,0) ve B(6,8) noktaları arasındaki uzaklık kaç birimdir?

A) 10
B) 8
C) 12
D) 6

✅ Çözüm:

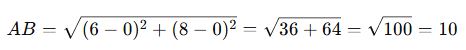
Cevap: A

2. Doğrunun Eğimi ve Eğim Açısı

A) Doğrunun Eğimi (m)

Koordinat düzleminde, bir doğru üzerindeki A(x1,y1) ve B(x2,y2) noktaları biliniyorsa, doğrunun eğimi şu formülle hesaplanır:

​​

✅ Notlar:

• Eğim, doğruyun x ekseniyle yaptığı açının tanjantıdır.

• Yatay doğruların eğimi 0, dikey doğruların eğimi tanımsızdır.

• Pozitif eğim: sağa yukarı çıkar, negatif eğim: sağa aşağı iner.

B) Eğim Açısı (α)

Doğrunun x ekseniyle pozitif yönde yaptığı açının ölçüsüne eğim açısı denir.

Yani eğimi bilinen bir doğrunun eğim açısı:

Örnek:

A(1,2) ve B(4,6) noktalarından geçen doğrunun eğimi:

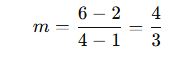
Örnek Soru:

A(2,5) ve B(6,9) noktalarından geçen doğrunun eğimi kaçtır?

A) 2
B) 1
C) 4
D) 1/2​

✅ Çözüm:

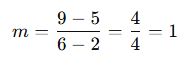
Cevap: B

3. Doğrunun Denklem Türleri

📌 A) Eğim–Nokta Formu

Eğimi $m$, bir noktası (x1,y1) olan doğrunun denklemi:

✅ Örnek:
Eğimi 2, noktası (1, 3) olan doğrunun denklemi:

B) İki Nokta Arasından Geçen Doğru

A(x1,y1) ve B(x2,y2) noktalarından geçen doğrunun denklemi:

​​

Bu eşitlikler sağlandığında, tüm noktalar doğru üzerindedir.

C) Y Ekseni Kestiği Nokta Bilinen Doğru (Y = mx + n)

Bu tür doğruların denklemi genel olarak:

Burada:

• m: eğim

• n: doğrunun y-eksenini kestiği noktadır.

Örnek:

A(0,2) ve B(4,6) noktalarından geçen doğrunun denklemini bulalım.

1. Eğimi:

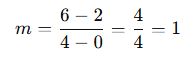
2. Eğim–nokta formu:

4. Doğruların Birbirine Göre Durumları

Koordinat düzlemindeki iki doğrunun konumu, eğimlerine bakılarak belirlenir. İki doğrunun genel denklemi şu şekildedir:

​

📌 A) Paralel Doğrular

Eğimleri eşit, y-kesişimleri farklı olan doğrular:

​

✅ Örnek:

→ Paralel doğrular

B) Dik Doğrular

Eğimlerinin çarpımı -1 olan doğrular:

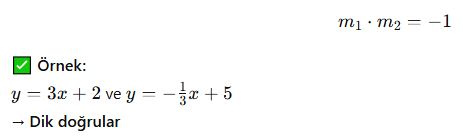
C) Çakışık Doğrular

Eğimleri ve y-kesişimleri eşit olan doğrular:

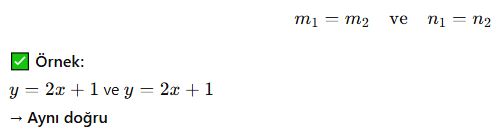
Örnek Soru:

Aşağıdaki doğrulardan hangileri birbirine diktir?

5. Bir Noktanın Doğruya Uzaklığı

Koordinat düzleminde bir A(x0,y0) noktasının,

denklemine sahip bir doğruya olan dik uzaklığı:

​​

Bu formül, noktanın doğruya olan en kısa mesafesini, yani dik uzaklığı verir.

Örnek:

10. Sınıf Matematik – Analitik İnceleme Testi

Cevap Anahtarı:

1. B

2. A

3. A

4. B

5. D

6. B

7. C (tan⁻¹(3) ≈ 71.6°)

8. C

9. A

10. B (x = sabit → dikey doğru → eğim tanımsız)